
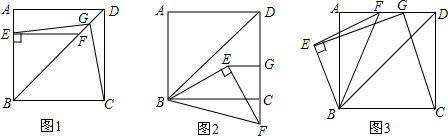
分析 (1)过点G作GH⊥BD于G交CD于H,通过条件证明△HGE≌△ICG,就可以得出结论EG=CG,EG⊥CG;
(2)过点E作EH⊥BC交BC于点H,易证出△EHB≌△EGF,即可得出EG=CG,EG⊥CG;
(3)特殊情况,如图3,过点E作EH⊥AD交AD的延长线于点H,作EM⊥BC,交BC的延长线于点M,易证出△EHF≌△BME,再证出△GHE≌△CDG即可得出结论.
一般情况,如图4,过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,再判断出∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC,易得△MEC是等腰直角三角形,即可得出EG=CG,EG⊥CG.
解答 证明:(1)EG=CG,且EG⊥CG.
如图,过GH⊥AB于点H,延长HG交CD于点I,作GK⊥AD于点K.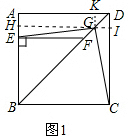
则四边形GIDK是正方形,四边形AKGH是矩形,
∴AK=HG,KD=DI=GI=AH,
∵AD=CD,
∴IC=HG,
∵AD∥GH∥EF,G是DF的中点,
∴HA=HE,
∴HE=GI,
∵在Rt△HGE和Rt△ICG中,
$\left\{\begin{array}{l}{HE=GI}\\{∠GHE=∠CIG}\\{HG=IC}\end{array}\right.$,
∴Rt△HGE≌Rt△ICG(SAS),
∴EG=CG,∠HGE=∠GCI,∠HEG=∠CGI,
∴∠HGE+∠CGI=90°,
∴∠EGC=90°,
∴EG⊥CG;
(2)EG=CG,且EG⊥CG.
如图2,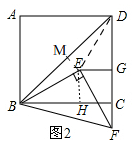
连接DE,过点E作EM⊥BD于M,
∵四边形ABCD是正方形,
∴∠BCF=∠BME=90°,
∵BD是正方形ABCD的对角线,
∴BD=$\sqrt{2}$BC,∠CBD=45°,
由旋转知,∠EBF=45°,
∴∠EBM=∠CBF,
∵∠BME=∠BCF=90°,
∴△BME∽△BCF,
∴$\frac{BM}{BC}=\frac{BE}{BF}$,
∵△BEF是等腰直角三角形,
∴BF=$\sqrt{2}$BE,
∴BC=$\sqrt{2}$BM,
∴BD=$\sqrt{2}$×$\sqrt{2}$BM=2BM,
∴BM=DM,
∵EM⊥BD,
∴BE=DE,
∵BE=EF,
∴DE=EF,
∵点G是DF的中点,
∴EG⊥CG
过点E作EH⊥BC交BC于点H,
∴HE⊥EG,
∵∠BEH+∠HEF=90°,∠FEG+∠HEF=90°,
∴∠BEH=∠FEG,
在△EHB和△EGF中,
$\left\{\begin{array}{l}{∠EHB=∠EGF}\\{∠BEH=∠FEG}\\{BE=FE}\end{array}\right.$,
∴△EHB≌△EGF(AAS),
∴EH=EG,
∴四边形EHCG是正方形,
∴EG=CG,且EG⊥CG;
方法2、如图,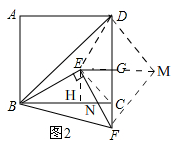
延长EG至M使GM=GE,连接DE,DM,FM,CE,
∵点G是DF的中点,
∴DG=FG,
∴四边形DEFM是平行四边形,
∴DM=EF,∠CDM=∠CFE,
∵∠CFE+∠CNF=90°,
∴∠CDM+∠CNF=90°,
∵∠CNF=∠BNE,
∴∠CDM+∠BNE=90°,
∵∠EBN+∠BNE=90°,
∴∠CBE=∠CDM,
∵BE=EF,
∴BE=DM,
在△CBE和△CDM中,$\left\{\begin{array}{l}{BE=DM}\\{∠CBE=∠CDM}\\{BC=CD}\end{array}\right.$,
∴△CBE≌△CDM,
∴CE=CM,
∵GE=GM,
∴△ECM是等腰三角形,
∴CG⊥EG,
过点E作EH⊥BC交BC于点H,
∴HE⊥EG,
∵∠BEH+∠HEF=90°,∠FEG+∠HEF=90°,
∴∠BEH=∠FEG,
在△EHB和△EGF中,
$\left\{\begin{array}{l}{∠EHB=∠EGF}\\{∠BEH=∠FEG}\\{BE=FE}\end{array}\right.$,
∴△EHB≌△EGF(AAS),
∴EH=EG,
∴四边形EHCG是正方形,
∴EG=CG,且EG⊥CG;
(3)EG=CG,且EG⊥CG.
特殊情况,如图3,如果旋转到点F落在AD上时,
过点E作EH⊥AD交AD的延长线于点H,作EM⊥BC,交BC的延长线于点M,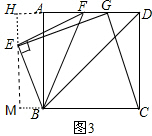
∵∠HEF+∠MEB=90°,∠EBM+∠MEB=90°,
∴∠HEF=∠EBM,
在△EHF和△BME,
$\left\{\begin{array}{l}{∠H=∠M}\\{∠HEF=∠EBM}\\{EF=BE}\end{array}\right.$
∴△EHF≌△BME(AAS),
∴HE=BM,ME=HF,
∵AF+DF=ME+EH,即AF+DF=AF+2HE,且点G是FD的中点,
∴HE=DG,
∴HF+FG=AD=CD,
在△GHE和△CDG,
$\left\{\begin{array}{l}{HE=GD}\\{∠H=∠GDC}\\{HG=CD}\end{array}\right.$
∴△GHE≌△CDG(SAS),
∴EG=CG,且EG⊥CG.
一般情况,如图4,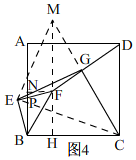
过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.记EF交AB于P,
∴∠MFN=90°,
∵G为FD中点,易证△CDG≌△MFG,得到CD=FM,
∵BC=CD,
∴BC=FM,
∵∠BNF=∠ABC=90°,∠BPE=∠FPN,
∴∠ABE=∠EFN,
∴∠ABE+∠ABC=∠EFN+∠MFN,
∴∠EBC=∠EFM,
∵BE=EF
∴△EFM≌△EBC,
∴∠FEM=∠BEC,EM=EC
∵∠FEC+∠BEC=90°,
∴∠FEC+∠FEM=90°,即∠MEC=90°,
∴△MEC是等腰直角三角形,
∵G为CM中点,
∴EG=CG,EG⊥CG.
点评 本题主要考查了四边形综合题,涉及三角形全等的判定及性质,正方形的性质等知识,解题的关键是构造三角形全等.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,
如图,?ABCD的对角线AC、BD相交于点O,△OAB是等边三角形,且AB=4,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{π}{2}$)0=1 | B. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | C. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | D. | (-3)-1=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com