
 ��ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��4��m���ڱ�AB�ϣ�����������y=$\frac{k}{x}$��k��0���ڵ�һ�����ڵ�ͼ����D��E����cos��BOA=$\frac{4}{5}$��
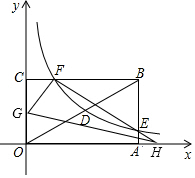
��ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��4��m���ڱ�AB�ϣ�����������y=$\frac{k}{x}$��k��0���ڵ�һ�����ڵ�ͼ����D��E����cos��BOA=$\frac{4}{5}$������ ��1���ɾ��ε����ʿ����OA�������Ǻ�����������OB��������AB�ij���
��2�������������D�����꣬���뷴������������ʽ������������ʽ����E������������ʽ�����m��ֵ��
��3���ɷ�������������ʽ�����F�����꣬������CF�ij�����OG=x������������ȫ�ȵ����ʿɱ�ʾ��CG��FG����Rt��CGF�����ù��ɶ����ɵõ����̣������OG�ij���
��� �⣺
��1���ߵ�E��4��m���ڱ�AB�ϣ�
��OA=4��
��Rt��AOB��
��cos��BOA=$\frac{4}{5}$��
��OB=5��
��AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=3��
��2���ɣ�1�����ɵõ�B������Ϊ��4��3����
�ߵ�DΪOB���е㣬
���D��2��1.5����
�ߵ�D�ڷ���������$y=\frac{k}{x}$��k��0����ͼ���ϣ�
��k=3��
�෴������������ʽΪ$y=\frac{3}{x}$��
�֡ߵ�E��4��n���ڷ���������ͼ���ϣ�
��$m=\frac{3}{4}$��
��3�����F��a��3����
�߷�����������ͼ������εı�BC���ڵ�F��
��a=1��
��CF=1��
��OG=x��
�ߡ�OGH�ա�FGH��
��OG=FG=x��CG=3-x��
��Rt��CGF��
�ɹ��ɶ����ɵ�GF2=CF2+CG2��
��x2=��3-x��2+12��
���x=$\frac{4}{3}$��
��OG=$\frac{4}{3}$��
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ���������ɶ��������Ǻ����Ķ��塢���ε����ʡ�ȫ�������ε����ʼ�����˼�룮�ڣ�1�����������Ǻ����Ķ������OB�ij��ǽ���Ĺؼ����ڣ�2�������þ��ε��������D�������ǽ���Ĺؼ����ڣ�3������OG�ij��ֱ��ʾ��CG��FG�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
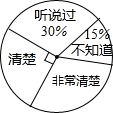 ��ʮ����ȫ���˴��Ĵλ�������ͨ���ġ��л��������Ʒ������ڽ���9��1����ʽʵʩ��Ϊ���˽����Դ��Ʒ���֪�������ij�ֵ����Ͻ�����������ѡȡ��900��������е��飬���������������������²�������ͳ��ͼ�ͱ���
��ʮ����ȫ���˴��Ĵλ�������ͨ���ġ��л��������Ʒ������ڽ���9��1����ʽʵʩ��Ϊ���˽����Դ��Ʒ���֪�������ij�ֵ����Ͻ�����������ѡȡ��900��������е��飬���������������������²�������ͳ��ͼ�ͱ���| ��˵�� | ��֪�� | ��� | �dz���� |
| A | B | 225 | C |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-5=b-5 | B�� | a+3=b+3 | C�� | 2a=2b | D�� | $\frac{a}{c}$=$\frac{b}{c}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
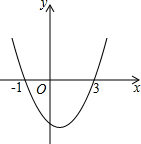 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������x�����������ֱ�Ϊ��-1��0������3��0���������������⣺��b-2a=0����abc��0����4a+2b+c��0����8a+c��0��������ȷ���У�������
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������x�����������ֱ�Ϊ��-1��0������3��0���������������⣺��b-2a=0����abc��0����4a+2b+c��0����8a+c��0��������ȷ���У�������| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ��O�ཻ�ڵ�D����֤��DE=DB��
��ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ��O�ཻ�ڵ�D����֤��DE=DB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com