练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．先化简，再求值：$\frac{{x}^{2}-2x}{x}$÷（x-$\frac{4}{x}$），其中x=$\sqrt{3}$-2．

    分析 首先把所求的分式分子、分母分解因式，把除法转化为乘法，然后进行约分，再通分、进行分式的加减运算即可化简，然后代入x的值求解．

    解答 解：原式=$\frac{x（x-2）}{x}$÷$\frac{{x}^{2}-4}{x}$
    =（x-2）•$\frac{x}{（x+2）（x-2）}$
    =$\frac{x}{x+2}$．
    当x=$\sqrt{3}$-2时，原式=$\frac{\sqrt{3}-2}{\sqrt{3}}$=$\frac{3-2\sqrt{3}}{3}$．

    点评 本题考查了分式的化简求值，正确进行通分、约分是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

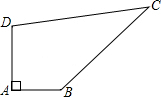    4．如图，某开发区计划在一块四边形的空地ABCD上种植草坪，已知∠A=90°，AB=4m，BC=12m，CD=13m，DA=3m，种植每平方米草皮的预算费用为300元，若第一年对草坪的保养费用占种植草皮总预算的4%，以后每年的保养费用都将在前一年的基础上递增2%，求第三年的草坪保养费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，某小区规划在一个长20米、宽10米的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草．要使每一块花草的面积都为27平方米，那么通道的宽应设计成多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，现有一个边长是1的正方形ABCD，在它的左侧补一个矩形ABEF，使所得矩形CEFD∽矩形ABEF，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

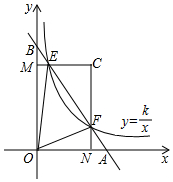    9．如图，平面坐标系中，AB交矩形ONCM于E、F，若$\frac{BE}{BF}$=$\frac{1}{m}$（m＞1），且双曲线y=$\frac{k}{x}$也过E、F两点，记S△CEF=S1，S△OEF=S2，用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

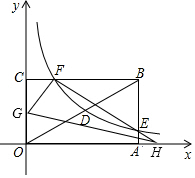    19．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，m）在边AB上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限内的图象经过点D、E，且cos∠BOA=$\frac{4}{5}$．
    （1）求边AB的长；
    （2）求反比例函数的解析式和m的值；
    （3）若反比例函数的图象与矩形的边BC交于点F，点G、H分别是y轴、x轴上的点，当△OGH≌△FGH时，求线段OG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知点A（4，y1），B（$\sqrt{2}$，y2），C（-2，y3）都在二次函数y=-2x2的图象上，则y1，y2，y3的大小关系是（　　）
    A．y1＞y2＞y3B．y2＞y3＞y1C．y3＞y2＞y1D．y2＞y1＞y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．画出数轴，把下列各数分别在数轴上表示出来，并用“＜”连接起来：2，0，-3，|-3.5|，-4$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

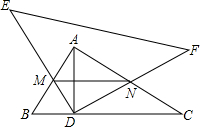    4．如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，AD是BC边上的高，以D为直角顶点的Rt△DEF绕点旋转，在旋转过程中，DE、EF分别与边AB、AC交于点M、N，则线段MN的最大值与最小值的差为$\frac{16}{5}$．

    查看答案和解析>>

    同步练习册答案