
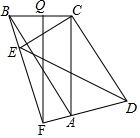
 △ABC中,∠ACB=90°,BC=2,AC=4,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于F点,在旋转过程中,△ABF的面积的最大值是5.
△ABC中,∠ACB=90°,BC=2,AC=4,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于F点,在旋转过程中,△ABF的面积的最大值是5. 分析 设∠BCE=∠ACD=α,可得∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,根据四边形内角和可得∠BFA=90°,由勾股定理求得AF2+BF2=AB2=20,从而知AF2+BF2≥2AF•BF,即AF•BF≤$\frac{A{F}^{2}+B{F}^{2}}{2}$=10,继而得S△ABF=$\frac{1}{2}$AF•BF≤5.
解答 解:∵△DEC是由△ABC绕C点旋转得到,
∴CE=CB,CD=CA,∠BCE=∠ACD,
设∠BCE=∠ACD=α,
∴∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,
∴在四边形BCDP中,∠BFA=360°-90°-α-2(90°-$\frac{1}{2}$α)=90°,
∵在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴AF2+BF2=AB2=20,
∵AF2+BF2≥2AF•BF,
∴AF•BF≤$\frac{A{F}^{2}+B{F}^{2}}{2}$=10,
∴S△ABF=$\frac{1}{2}$AF•BF≤5,即△ABF的面积的最大值是5,
故答案为:5.
点评 本题主要考查旋转的性质、直角三角形的性质及勾股定理,解题的关键是根据四边形内角和得出∠BPA=90°.


科目:初中数学 来源: 题型:选择题
| A. | 70千米/小时 | B. | 75千米/小时 | C. | 80千米/小时 | D. | 85千米/小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形中最大的内角不能小于60° | |
| B. | 三角形的外角一定大于和它相邻的内角 | |
| C. | 等边三角形是轴对称图形,它的对称轴有3条 | |
| D. | 三角形的一条中线把该三角形分成面积相等的两个部分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com