
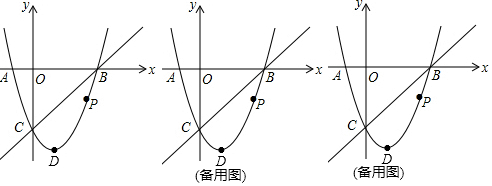
���� ��1��ֱ����ɶ���ʽ���ɵó������߽���ʽ��
��2����ȷ������B��C���꣬�ٸ���ͼ��ֱ��д����Χ��
��3���������ε����ʵó�PO=PC���ɵó���P�������꣬���������߽���ʽ���ɵó����ۣ�
��4������������ϵ�м���ͼ�ε�����ļ��㷽������������ϵʽ���������������ֵ��
��5�������ֱ��BC��BC��CD�Ľ���ʽ������������������ε����ʣ�һ��Ա�ƽ�м��ɵó�ֱ��DP1��CP2��BP3�Ľ���ʽ���ֱ����������ߵĽ���ʽ������������⼴�ɣ�
��� �⣺��1���ߵ�D��1��-4����������y=x2+bx+c�Ķ��㣬
��y=��x-1��2-4=x2-2x-3��
�ʴ�Ϊy=x2-2x-3��
��2����x=0��
��y=-3��
��C��0��-3����
��y=0����x2-2x-3=0��
��x=-1��x=3��
��A��-1��0����B��3��0����
���ʽx2+bx+c��kx+m�Ľ⼯Ϊx��0��3��
�ʴ�Ϊx��0��3��
��3����ͼ1����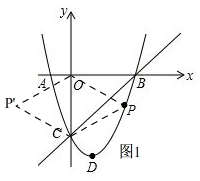 �ı���POP��CΪ���Σ�
�ı���POP��CΪ���Σ�
��PO=PC��
��C��0��-3����
���P��������Ϊ-$\frac{3}{2}$��
��P��������y=x2-2x-3�ϣ�
��-$\frac{3}{2}$=x2-2x-3��
��x=$\frac{2+\sqrt{10}}{2}$��x=$\frac{2-\sqrt{10}}{2}$���ᣩ��
��P��$\frac{2+\sqrt{10}}{2}$��-$\frac{3}{2}$����
��4����ͼ2���ɣ�1��֪��B��3��0����C��0��-3����
��ֱ��BC�Ľ���ʽΪy=x-3��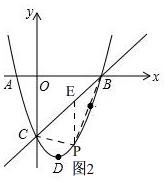 ����P��PE��y�ύBC��E��
����P��PE��y�ύBC��E��
��P��m��m2-2m-3������0��m��3��
��E��m��m-3����
��PE=m-3-��m2-2m-3��=-m2+3m��
��A��-1��0����B��3��0����C��0��-3����
��S�ı���ABPC=S��ABC+S��PCE+S��PBE
=$\frac{1}{2}$AB•OC+$\frac{1}{2}$PE•|xP|+$\frac{1}{2}$PE•|xB-xP|
=$\frac{1}{2}$AB•OC+$\frac{1}{2}$PE��|xP|+|xB-xP|��
=$\frac{1}{2}$��4��3+$\frac{1}{2}$��-m2+3m������m+3-m��
=6+$\frac{1}{2}$����-m2+3m��
=-$\frac{1}{2}$��m2-3m��+6
=-$\frac{1}{2}$��m-$\frac{3}{2}$��2+$\frac{57}{8}$��
��m=$\frac{3}{2}$ʱ��S�ı���ABPC���=$\frac{57}{8}$��
��5����ͼ���ɣ�1��֪��B��3��0����C��0��-3����D��1��-4����
��ֱ��BC�Ľ���ʽΪy=x-3��ֱ��BD�Ľ���ʽΪy=2x-6��ֱ��CD�Ľ���ʽΪy=-x-3��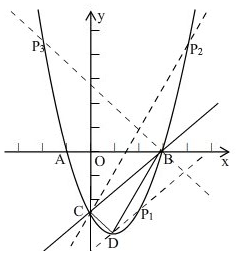 ����P��C��D��BΪ������ı���Ϊ���Σ�
����P��C��D��BΪ������ı���Ϊ���Σ�
�������ߵĽ���ʽΪy=x2-2x-3�٣�
�ٵ�DP1��BCʱ��
��ֱ��DP1�Ľ���ʽΪy=x-5�ڣ�
�����٢ڽ�ã���P1��2��-3����[��һ����Ϊ��1��-4���͵�D�غϣ���ȥ]
�ڵ�CP2��BDʱ����ֱ��CP2�Ľ���ʽΪy=2x-3�ۣ�
�����٢۽�õ�P2��4��5��
�۵�BP3��CDʱ����ֱ��BP3��CD�Ľ���ʽΪy=-x+3�ܣ�
�����٢ܽ�õ�P3��-2��5����
������P��C��D��BΪ������ı���Ϊ����ʱ����P������Ϊ��-2��5������2��-3����4��5����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ�����������߽���ʽ��������ͼ�ε�����ļ��㷽�������ε����ʣ����ε����ʣ��Ȿ��Ĺؼ����÷��̻����˼�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ������30����������������� | |
| B�� | ������֮�ȶ�����2��3������������ | |
| C�� | ����һ������120����������������� | |
| D�� | ����һ������ֱ�ǵ����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+2��y+2 | B�� | -2x��-2y | C�� | 1-x��1-y | D�� | $\frac{x}{2}��\frac{y}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У���D=60�㣬EΪ�߶�CD��һ�㣬����BE�����߶�BC��ֱ��BE���۽��Խ���AC�ڵ�F������EF�����FEB�ĽǶ�Ϊ30�㣮
��ͼ������ABCD�У���D=60�㣬EΪ�߶�CD��һ�㣬����BE�����߶�BC��ֱ��BE���۽��Խ���AC�ڵ�F������EF�����FEB�ĽǶ�Ϊ30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com