练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC∽△DEF，相似比为1：2．若BC=1，则EF的长是（　　）

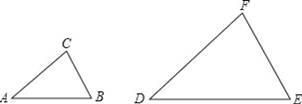
    A．1       B．2       C．3       D．4

    　


    B 【考点】相似三角形的性质．

    【分析】根据相似三角形对应边的比等于相似比即可求解．

    【解答】解：∵△ABC∽△DEF，相似比为1：2，

    ∴=，

    ∴EF=2BC=2．

    故选：B．

    【点评】本题考查了相似三角形的性质：相似三角形对应边的比等于相似比．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，则圆锥的高是(     )

    A．4       B．4  C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


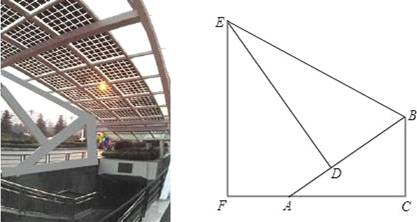
    如图是某地下商业街的入口，数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF．经测量，支架的立柱BC与地面垂直，即∠BCA=90°，且BC=1.5m，点F、A、C在同一条水平线上，斜杆AB与水平线AC的夹角∠BAC=30°，支撑杆DE⊥AB于点D，该支架的边BE与AB的夹角∠EBD=60°，又测得AD=1m．请你求出该支架的边BE及顶端E到地面的距离EF的长度．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    方程（x﹣3）2+4x（x﹣3）=0的解为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


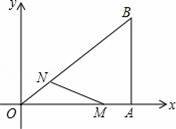
    如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：

    （1）求点N的坐标（用含x的代数式表示）；

    （2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？

    （3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，C，D两点在⊙O上，若∠BCD=40°，则∠ABD的度数为（　　）

    A．40°   B．50°    C．80°   D．90°

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，CD是边AB上的高，且=．

    （1）求证：△ACD∽△CBD；

    （2）求∠ACB的大小．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，则m=           。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：x2+2x﹣3（x2﹣x），其中x=﹣．

    查看答案和解析>>

    同步练习册答案