
【题目】已知:![]() 中,
中,![]() .
.
![]() 如图1,若
如图1,若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求AD的长;
,求AD的长;
![]() 如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于
如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于![]() 注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注
注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注![]()
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ;(2)
;(2)![]() 的解为
的解为![]() ;
;
(3)![]() 的解为
的解为![]() ;…………
;…………
解答下列问题:
(1)请猜想:方程![]() 的解为;
的解为;
(2)请猜想:关于![]() 的方程
的方程![]() 的解为
的解为![]() (a≠0);
(a≠0);
(3)下面以解方程![]() 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.
解:原方程可化为![]() .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点Q是CD边的中点,过点Q作AQ⊥PQ交BC于P,(1)证明:△ADQ ∽△QCP;(2)若PC=1,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲品牌手机四月份售价比三月份每台降价500元.如果卖出相同数量的甲品牌手机,那么三月份销售额为9万元,四月份销售额只有8万元.
(1)四月份甲品牌手机每台售价为多少元?
(2)为了提高利润,该店计划五月份购进甲品牌及乙品牌手机销售,已知甲每台进价为3500元,乙每台进价为4000元,预算用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,问按此预算要求,可以有几种进货方案,请写出所有进货方案?
(3)该店计划五月在销售甲品牌手机时,在四月份售价基础上每售出一台甲品牌手机再返还顾客现金![]() 元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
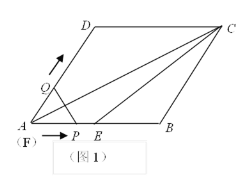
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A—D—C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
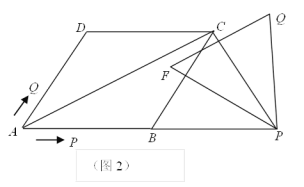
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α ° (0<α<360°),直线PF 分别与直线AC、直线CD交于点M、N.是否存在这样的α ,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=﹣x2+bx+c的图象的最高点是(﹣1,﹣3),则b、c的值分别是( )
A. b=2,c=4 B. b=﹣2,c=﹣4 C. b=2,c=﹣4 D. b=﹣2,c=4
查看答案和解析>>
科目:初中数学 来源: 题型:
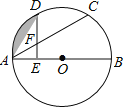
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菜农李伟种植的某蔬菜计划以每千克![]() 元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克
元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克![]() 元的单价对外批发销售.
元的单价对外批发销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 小华准备到李伟处购买
小华准备到李伟处购买![]() 吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金![]() 元.
元.
试问小华选择哪种方案更优惠,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com