
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先求出△的值,再根据△的意义即可得到结论;
(2)先利用公式法求出方程的解为x1=2,x2=k-1,然后分类讨论当AB=BC或AC=BC时△ABC为等腰三角形,然后求出k的值.
解:(1)证明:△=b2-4ac=[-(k+1)]2-4×(2k-2)=k2-6k+9=(k-3)2,
∵(k-3)2≥0,即△≥0,
∴此方程总有两个实数根;
(2)解:一元二次方程x2-(k+1)x+2k-2=0的解为x=![]() ,即x1=2,x2=k-1,
,即x1=2,x2=k-1,
当AB=2,AC=k-1,且AB=AC时,△ABC是等腰三角形,则k-1=3,k=4,
当AB=2,AC=k-1,且AC=BC时,△ABC是等腰三角形,则k-1=2,解得k=3,
综合上述,k的值为3或4.


科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年淘宝网都会举办“双十一”购物活动,许多商家都会利用这个契机进行打折让利的促销活动.甲网店销售一件A商品成本为50元,网上标价80元.
(1)“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买主,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?
(2)据媒体爆料,有一些淘宝商家在“双十一”购物活动当天,先提高商品的网上标价后再推出促销活动,存在欺诈行为.“双十一”活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出1000件A商品.在“双十一”购物活动这天,乙网店先将网上标价提高a%,再推出五折销售的促销活动,吸引了大量网购者,乙网店在“双十一”购物活动当天卖出的A商品数量也比原来一周卖出的A商品数量增加了2a%,这样“双十一”活动当天乙网店的利润达到了2万元,求乙网店在“双十一”购物活动这天的网上标价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
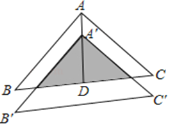
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为18,阴影部分三角形的面积为8.若AA'=1,则A'D等于 ( )
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() .
.
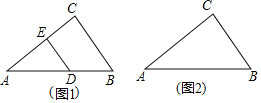
![]() 如图1,若
如图1,若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求AD的长;
,求AD的长;
![]() 如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于
如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于![]() 注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注
注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com