
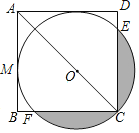
【题目】如图,O为正方形ABCD的对角线AC上一点,以O为圆心,OC的长为半径的![]() 与AB相切于点M.
与AB相切于点M.
![]() 求证:AD与
求证:AD与![]() 相切;
相切;
![]() 若
若![]() ,求图中阴影部分面积.
,求图中阴影部分面积.
【答案】(1)见解析;(2)2π-4.
【解析】
(1)过O作ON⊥AD于N,由垂直的定义得到∠ONA=90°,根据正方形的性质得到∠OAN=∠OAM=45°,根据切线的性质得到∠OMA=90°,根据全等三角形的性质得到ON=OM,于是得到结论;
(2)首先求出AE=AF,进而求出△CEF的面积,进而得出阴影部分的面积.
解: (1)证明:连接OM,过O作ON⊥AD于N,
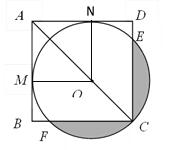
∴∠ONA=90°,
∵四边形ABCD是正方形,
∴∠OAN=∠OAM =45°,
∵AB与⊙O相切于M,
∴∠OMA=90°,
在△ONA与△OMA中,
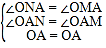 ,
,
∴△ONA≌△OMA,
∴ON=OM,
∴BC与⊙O相切;
(2)设⊙O的半径为r.
显然OM∥CB,
∴△AOM∽△ACB,
∴ ![]() ,即
,即![]() ,
,

解得r=2
故⊙O的半径为2;
连接EF,

则EF是⊙O的直径,
∵AC是正方形ABCD的对角线,
∴∠DAC=45°,
∵CO=FO,
∴∠CFO=45°,
∴∠COF=90°,
则AE=AF,
∵EF=4,
∴CE=CF=2![]() ,
,
∴S△CEF=![]() ×2
×2![]() ×2
×2![]() =4,
=4,![]() =
=![]() =
=![]() ,
,
故阴影部分面积: ![]() -4.
-4.


科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
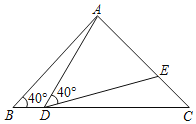
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.
(1)当∠BDA=115°时,∠BAD=_____°,∠DEC=_____°;当点D从B向C运动时,∠BDA逐渐变______(填”大”或”小”);
(2)当DC=AB=2时,△ABD与△DCE是否全等?请说明理由:
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=﹣x2+bx+c的图象的最高点是(﹣1,﹣3),则b、c的值分别是( )
A. b=2,c=4 B. b=﹣2,c=﹣4 C. b=2,c=﹣4 D. b=﹣2,c=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一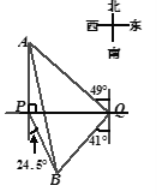 知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王涵想知道一堵墙上点![]() 的高度,即
的高度,即![]() 的长度
的长度![]() ,但点
,但点![]() 的位置较高,没有梯子之类的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
的位置较高,没有梯子之类的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
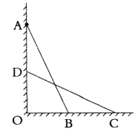
(1)补全方案.
第一步:如图,找一根长度大于![]() 的直杆,使直杆靠在墙上,且顶端与点
的直杆,使直杆靠在墙上,且顶端与点![]() 重合,记下直杆与地面的夹角
重合,记下直杆与地面的夹角![]() ;
;
第二步:使直杆顶端竖直缓慢下滑,直到![]() __________
__________![]() __________,标记此时直杆的底端点
__________,标记此时直杆的底端点![]() ;
;
第三步:测量__________的长度,即为点![]() 的高度;
的高度;
(2)说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com