
【题目】如图1,我们已经学过:点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
(1)证明点D是AB边上的黄金分割点;
(2)证明直线CD是△ABC的黄金分割线.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)证明AD=CD=BC,证明△BCD∽△BCA,得到![]() .则有
.则有![]() ,所以点D是AB边上的黄金分割点;
,所以点D是AB边上的黄金分割点;
(2)证明![]() ,直线CD是△ABC的黄金分割线;
,直线CD是△ABC的黄金分割线;
解:(1)点D是AB边上的黄金分割点.理由如下:
![]() AB=AC,∠A=
AB=AC,∠A=![]() ,
,![]() ∠B=∠ACB=
∠B=∠ACB=![]() .
.
![]() CD是角平分线,
CD是角平分线, ![]() ∠ACD=∠BCD=
∠ACD=∠BCD=![]() ,
,
![]() ∠A=∠ACD,
∠A=∠ACD,![]() AD=CD.
AD=CD.
![]() ∠CDB=
∠CDB=![]() 180-∠B-∠BCD=
180-∠B-∠BCD=![]() ,
,
![]() ∠CDB=∠B,
∠CDB=∠B,![]() BC=CD.
BC=CD.
![]() BC=AD.
BC=AD.
在△BCD与△BCA中, ∠B=∠B,∠BCD=∠A=![]() ,
,
![]() △BCD∽△BCA,
△BCD∽△BCA, ![]()
![]()
![]()
![]()
![]() 点D是AB边上的黄金分割点.
点D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.理由如下:
设ABC中,AB边上的高为h,则
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
由(1)得点D是AB边上的黄金分割点,![]()
![]()
![]() ,
,
![]() 直线CD是△ABC的黄金分割线
直线CD是△ABC的黄金分割线


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
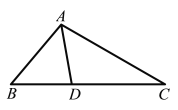
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=17,BC=21,AC=10,动点P从点C出发,沿着CB运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
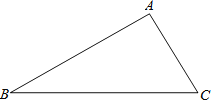
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )

A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为xcm,CF的长为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y/cm | 2.5 | 1.1 | 0 | 0.9 | 1.5 | 1.9 | 2 | 1.9 |
| 0.9 | 0 |
(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BE=CF时,BE的长度约为 cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com