
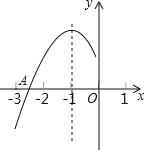
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①abc>0;②4ac﹣b2<0;③a+b+c>0;④3a<﹣c;⑤am2+bm≤a﹣b(m为任意实数).正确结论的个数是( )
A. 4B. 3C. 2D. 1
【答案】A
【解析】
根据二次函数的图像与性质依次判断即可.
解:由图象可得,
a<0,b<0,c>0,
∴abc>0,故①正确,
该函数图象与x轴有两个交点,则b2﹣4ac>0,即4ac﹣b2<0,故②正确,
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,
∴当x=1时,y=a+b+c<0,故③错误,
∵![]() =﹣1,得b=2a,
=﹣1,得b=2a,
∴当x=1时,y=a+b+c=a+2a+c<0,得3a<﹣c,故④正确,
∵当x=﹣1时,y=a﹣b+c取得最大值,
∴am2+bm+c≤a﹣b+c,即am2+bm≤a﹣b(m为任意实数),故⑤正确,
故选:A.


科目:初中数学 来源: 题型:
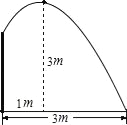
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
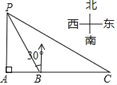
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-(a+b)x2-2cx+a-b,a、b、c是△ABC的三边
(1) 当抛物线与x轴只有一个交点时,判断△ABC是什么形状
(2) 当![]() 时,该函数有最大值
时,该函数有最大值![]() ,判断△ABC是什么形状
,判断△ABC是什么形状
查看答案和解析>>
科目:初中数学 来源: 题型:
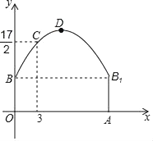
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线最高点D到墙面OB的水平距离为6m时,隧道最高点D距离地面10m.
(1)求该抛物线的函数关系式;
(2)一辆货运汽车载一长方体集装箱后宽为4m,高为6m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.
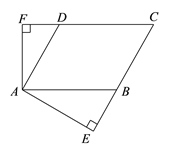
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.


(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com