
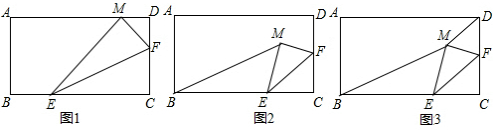
ЗжЮі ЃЈ1ЃЉШчЭМ1ЃЌзїENЁЭADгкЕуNЃЌгЩОиаЮЕФаджЪОЭПЩвдЕУГіEN=4ЃЌAN=3ЃЌгЩЙДЙЩЖЈРэОЭПЩвдЧѓГіMNЕФжЕЃЌНјЖјЧѓГіНсТлЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌЕБЁЯBME=90ЁуЪБЃЌгЩЁЯEMF=90ЁуЃЌОЭПЩвдЕУГіBЁЂMЁЂFдкЭЌвЛжБЯпЩЯЃЌгЩЙДЙЩЖЈРэОЭПЩвдЧѓГіBFЃЌЧѓГіBMЃЌдкRtЁїBMEжагЩЙДЙЩЖЈРэОЭПЩвдЧѓГіНсТлЃЛШчЭМ3ЃЌЕБЁЯBEM=90ЁуЪБЃЌЁЯMEC=90ЁуОЭПЩвдЕУГіЫФБпаЮECFMЪЧе§ЗНаЮЃЌжБНгЕУГіCEЕФжЕЃЛ
ЂкгЩЫФБпаЮABMDЕФжмГЄЕФзюаЁОЭвЊBM+MDзюаЁЃЎЕУГіBЁЂMЁЂDдкЭЌвЛжБЯпЩЯЃЌОЭгаЕуMдкBDЩЯЃЌСЌНсMCЃЌОЭПЩвдЕУГіEFДЙжБЦНЗжMCНЛEFгкЕуGЃЌОЭгаFGЪЧЁїMDCЕФжаЮЛЯпЃЌЕУГіGFЁЮBDЃЌОЭгаBE=ECНјЖјЕУГіНсТлЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1ЃЌзїENЁЭADгкЕуNЃЌ
ЁрЁЯANE=ЁЯENM=90ЁуЃЎ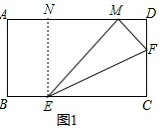
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=ЁЯB=ЁЯC=ЁЯD=90ЁуЃЌAB=CD=4ЃЌAD=BC=8ЃЌ
ЁрЁЯA=ЁЯB=ЁЯANE=90ЁуЃЌ
ЁрAB=NE=4ЃЌAN=BEЃЎ
ЁпEC=5ЃЌ
ЁрBE=3ЃЌ
ЁрAN=3ЃЎ
ЁпЁїEFCгыЁїEFMЙигкжБЯпEFЖдГЦЃЌ
ЁрЁїEFCЁеЁїEFMЃЌ
ЁрEC=EM=5ЃЎ
дкRtЁїEMNжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
MN=3ЃЌ
ЁрMD=8-3-3=2ЃЎ
Д№ЃКMDЕФГЄЮЊ2ЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌЕБЁЯBME=90ЁуЪБЃЌ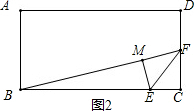
ЁпЁЯEMF=90ЁуЃЌ
ЁрЁЯBMF=180ЁуЃЌ
ЁрBЁЂMЁЂFдкЭЌвЛжБЯпЩЯЃЎ
ЁпFЪЧBCЕФжаЕуЃЌ
ЁрCF=DF=$\frac{1}{2}$CD=2ЃЎ
ЁпЁїEFCгыЁїEFMЙигкжБЯпEFЖдГЦЃЌ
ЁрЁїEFCЁеЁїEFMЃЌ
ЁрMF=CF=2ЃЌEC=EMЃЎ
дкRtЁїBCFжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
BF=2$\sqrt{17}$ЃЎ
ЁрBM=2$\sqrt{17}$-2ЃЎ
ЩшEC=EM=xЃЌдђBE=8-xЃЌдкRtЁїBMEжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
ЃЈ8-xЃЉ2-x2=ЃЈ2$\sqrt{17}$-2ЃЉ2ЃЌ
НтЕУЃКx=$\frac{\sqrt{17}-1}{2}$ЃЎ
ЁрCE=$\frac{\sqrt{17}-1}{2}$ЃЛ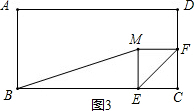
ШчЭМ3ЃЌЕБЁЯBEM=90ЁуЪБЃЌ
ЁрЁЯMEC=90Ёу
ЁпЁїEFCгыЁїEFMЙигкжБЯпEFЖдГЦЃЌ
ЁрЁїEFCЁеЁїEFMЃЌ
ЁрЁЯEMF=ЁЯC=90ЁуЃЌCF=FM=2ЃЌ
ЁрЫФБпаЮECFMЪЧе§ЗНаЮЃЌ
ЁрMF=CE=2ЃЎ
ЁрCE=2Лђ$\frac{\sqrt{17}-1}{2}$ЃЛ
ЂкШчЭМ4ЃЌЁпЫФБпаЮABMDЕФжмГЄзюаЁЃЌ
ЁрBM+MDзюаЁЃЌ
ЁрBЁЂMЁЂDдкЭЌвЛжБЯпЩЯЃЌ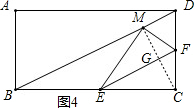
ЁрЕуMдкBDЩЯЃЎ
СЌНсMCЃЌ
ЁпЁїEFCгыЁїEFMЙигкжБЯпEFЖдГЦЃЌ
ЁрЁїEFCЁеЁїEFMЃЌ
ЁрEC=EMЃЌFC=FMЃЎ
ЁрEFДЙжБЦНЗжMCЃЌ
ЁрMG=CGЃЌ
ЁрGFЪЧЁїCDMЕФжаЮЛЯпЃЌ
ЁрFGЁЮBDЃЌ
ЁрBE=CEЃЎ
ЁпBC=8ЃЌ
ЁрCE=4ЃЎ
дкRtЁїABDжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
BD=4$\sqrt{5}$ЃЎ
ЁрЫФБпаЮABMDЕФжмГЄЕФзюаЁжЕЮЊЃК4$\sqrt{5}$+4+8=4$\sqrt{5}$+12ЃЎ
Д№ЃКЫФБпаЮABMDЕФжмГЄЕФзюаЁжЕЮЊЃЈ4$\sqrt{5}$+12ЃЉЃЌДЫЪБCEЕФГЄЮЊ4ЃЎ
ЕуЦР БОЬтПМВщСЫОиаЮЕФаджЪЕФдЫгУЃЌШЋЕШШ§НЧаЮЕФХаЖЈМАаджЪЕФдЫгУЃЌЙДЙЩЖЈРэЕФдЫгУЃЌжсЖдГЦЕФаджЪЕФдЫгУЃЌе§ЗНаЮЕФаджЪЕФдЫгУЃЌЗжРрЬжТлЫМЯыЕФдЫгУЃЌНтД№ЪБдЫгУЙДЙЩЖЈРэЧѓНтЪЧЙиМќЃЎ


 ЬьЬьСЗПкЫуЯЕСаД№АИ
ЬьЬьСЗПкЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
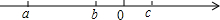 вбжЊaЁЂbЁЂcдкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЛЏМђ|a-b|-|b-c|+|c-a|ЃЎ
вбжЊaЁЂbЁЂcдкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЛЏМђ|a-b|-|b-c|+|c-a|ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com