
【题目】如图,在平面直角坐标系中,点![]() ,四边形
,四边形![]() 是正方形,作直线
是正方形,作直线![]() 与正方形
与正方形![]() 边所在直线相交于
边所在直线相交于![]()
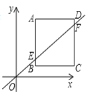
(1)若直线![]() 经过点
经过点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 平分正方形
平分正方形![]() 的面积,求
的面积,求![]() 的坐标;
的坐标;
(3)若![]() 的外心在其内部,直接写出
的外心在其内部,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 得
得![]() ,进而得
,进而得![]() ,根据待定系数法,即可得到答案;
,根据待定系数法,即可得到答案;
(2)设正方形的中心为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,从而求出点P的坐标,进而求出过点P的直线解析式:
,从而求出点P的坐标,进而求出过点P的直线解析式:![]() ,即可得到答案;
,即可得到答案;
(3)由![]() 的外心在其内部,得
的外心在其内部,得![]() 为锐角三角形.求出当直线
为锐角三角形.求出当直线![]() 经过点
经过点![]() 时所对应的k值,进而即可得到答案.
时所对应的k值,进而即可得到答案.
(1)![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ;
;
(2)当直线![]() 经过正方形的中心
经过正方形的中心![]() 时,平分正方形
时,平分正方形![]() 的面积.
的面积.
过点![]() 作
作![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,
,
易得:![]() ,
,
![]() ,
,
![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
将![]() 的横坐标
的横坐标![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ;
;
(3)![]() 的外心在其内部,
的外心在其内部,
![]() 为锐角三角形.
为锐角三角形.
当直线![]() 经过点
经过点![]() 时,
时,![]() 为直角三角形,
为直角三角形,
由(1)可知:![]() ,此时,
,此时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 为锐角三角形,
为锐角三角形,
即![]() 的外心在其内部,
的外心在其内部,![]() 的取值范围为:
的取值范围为:![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
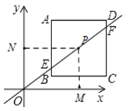
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
(1)求此抛物线的解析式;
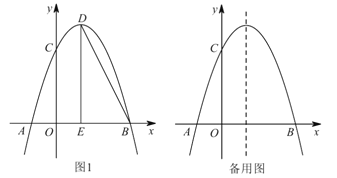
(2)点![]() 是抛物线上的动点,设点
是抛物线上的动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,
,![]() ,将
,将![]() 沿着
沿着![]() 翻折,得
翻折,得![]() ,若四边形
,若四边形![]() 恰好为正方形,直接写出
恰好为正方形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
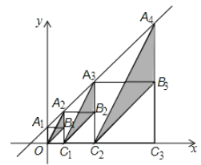
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,如图,作正方形
,如图,作正方形![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 轴上,将图中阴影部分三角形的面积从左到右依次记为
轴上,将图中阴影部分三角形的面积从左到右依次记为![]() ,则
,则
(1)![]() 的值为___________;
的值为___________;
(2)![]() 的值为___________.(含
的值为___________.(含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
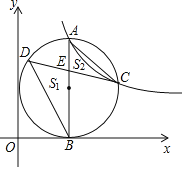
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
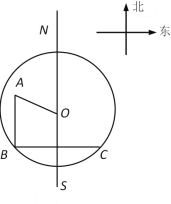
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°=![]() ,cos67.4°=
,cos67.4°=![]() ,tan67.4°=
,tan67.4°=![]() )
)
(1)求弦BC的长;
(2)请判断点A和圆的位置关系,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
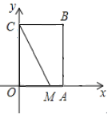
【题目】定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() ,点
,点![]() ,在边
,在边![]() 存在点
存在点![]() ,使得
,使得![]() 为“智慧三角形”,则点
为“智慧三角形”,则点![]() 的坐标为:______.
的坐标为:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
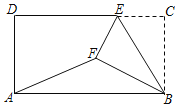
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com