
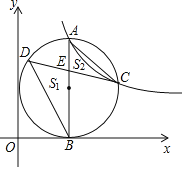
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
【答案】 等腰直角; ![]()
【解析】分析:
(1)如下图,连接O′C,过点C作CH⊥x轴于点H,由![]() O′和两坐标轴相切可知
O′和两坐标轴相切可知![]() O′和反比例函数
O′和反比例函数![]() 的图象都关于直线y=x对称,若设点A的坐标为(m,2m),则点C的坐标为(2m,m),结合题意易证四边形BHCO′是正方形,从而可得∠ABC=45°,由AB为
的图象都关于直线y=x对称,若设点A的坐标为(m,2m),则点C的坐标为(2m,m),结合题意易证四边形BHCO′是正方形,从而可得∠ABC=45°,由AB为![]() O′直径可得∠ACB=90°,由此可得△ABC是等腰直角三角形;
O′直径可得∠ACB=90°,由此可得△ABC是等腰直角三角形;
(2)由下图,连接DO′,并延长交BC于点F,由已知易得S1-S2=S△BCD-S△ABC, S△ABC是定值,BC是定值,从而可得当DF最长,即当DF⊥BC时,S1-S2的值最大,用含m的代数式表达出S△BCD和S△ABC的面积,结合S1-S2的最大值为1列出方程,解方程求得m的值即可得到点A的坐标,从而可得k的值.
详解:
(1)如下图,连接O′C,过点C作CH⊥x轴于点H,由![]() O′和两坐标轴相切可知
O′和两坐标轴相切可知![]() O′和反比例函数
O′和反比例函数![]() 的图象都关于直线y=x对称,
的图象都关于直线y=x对称,
∴若设点A的坐标为(m,2m),则点C的坐标为(2m,m),
∴BO′=CH=m,BO′∥CH,
∴四边形BHCO′是平行四边形,
∵BH=CH,∠BHC=90°,
∴四边形BHCO′是正方形.
∴∠ABC=45°,
∵AB为![]() O′直径,
O′直径,
∴∠ACB=90°,
∴△ACB是等腰直角三角形;
(2)由下图,连接DO′,并延长交BC于点F,
∵由图可得S1-S2=S△BCD-S△ABC, S△ABC是定值,BC是定值,
∴当DF最长,即当DF⊥BC时,S1-S2的值最大,
∵△ABC中,∠ACB=90°,∠ABC=45°,AB=2m,且DF⊥BC,
∴BC=AC=![]() ,DF=DO′+O′F=
,DF=DO′+O′F=![]() ,
,
又∵S1-S2=S△BCD-S△ABC=1,
∴![]() ,
,
化简得:![]() ,
,
∵点A(m,2m)在反比例函数函数![]() 的图象上,
的图象上,
∴k=2m2=![]() .
.
故答案为:(1)等腰直角;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,有边长为a的正方形卡片①,边长为b的正方形卡片②,两邻边长分别为a,b的矩形卡片③若干张.
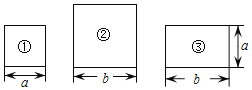
(1)请用2张卡片①,1张卡片②,3张卡片③拼成一个矩形,在方框中画出这个矩形的草图;
(2)请结合拼图前后面积之间的关系写出一个等式;
(3)小明想用类似方法解释多项式乘法(a+3b)(2a+2b)的结果,那么需用卡片①______张,卡片②______张,卡片③______张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种新型产品,每件成本为![]() 元.产品按质量分为
元.产品按质量分为![]() 个等级(每个月能生产同等级的产品),第一等级(最低等级)的产品能生产
个等级(每个月能生产同等级的产品),第一等级(最低等级)的产品能生产![]() 万件,每件以
万件,每件以![]() 元销售.每提搞一个等级,每件销售单价就提高
元销售.每提搞一个等级,每件销售单价就提高![]() 元,但产量减少
元,但产量减少![]() 万件.设生产该商品的质为第
万件.设生产该商品的质为第![]() 等级(
等级(![]() 为整数,且
为整数,且![]() ),产品的月总利润为
),产品的月总利润为![]() 元.
元.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)生产该产品的质量为第几等级时,月总利润最大,最大利润是多少?
(3)该商品在生产过程中,共有几个等级的产品销售的利润不低于![]() 万元.
万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
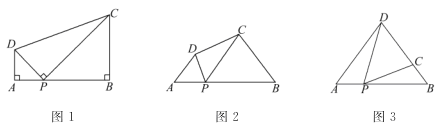
【题目】(1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD·BC=AP·BP.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当DC的长与△ABD底边上的高相等时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用礼花发射器发射彩纸礼花,每隔1.6秒发射一花弹,每束花弹发射的飞行路径,花弹爆炸的高度均相同,小明发射的第一束花弹的飞行高度![]() 米与飞行时间
米与飞行时间![]() 秒变化的规律如下表:
秒变化的规律如下表:
| 0 | 0.5 | 1 | 2 | 2.5 | 3 | …… |
| 1.5 |
| 2.75 | 3.5 |
| 3.75 | …… |
(1)根据表格中的数据选择适当的函数来表示![]() 与
与![]() 之间的关系,求出相应的函数解析式;
之间的关系,求出相应的函数解析式;
(2)当![]() 时,第一花束飞行到最高点,此时的高度为
时,第一花束飞行到最高点,此时的高度为![]() ,在
,在![]() 的情况下,求
的情况下,求![]() 的表达式,并判断这个表达式的变化趋势,若有变化,请说明变化过程,若是定值请求出这个定值;
的表达式,并判断这个表达式的变化趋势,若有变化,请说明变化过程,若是定值请求出这个定值;
(3)为了安全,要求花弹爆炸的高度不低于3米,小明发现在第一束花弹爆炸的同时,第三束花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,四边形
,四边形![]() 是正方形,作直线
是正方形,作直线![]() 与正方形
与正方形![]() 边所在直线相交于
边所在直线相交于![]()
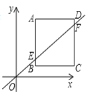
(1)若直线![]() 经过点
经过点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 平分正方形
平分正方形![]() 的面积,求
的面积,求![]() 的坐标;
的坐标;
(3)若![]() 的外心在其内部,直接写出
的外心在其内部,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
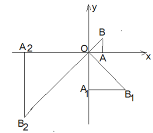
【题目】如图,在平面角坐标系xOy中,有一个等腰直角三角形△AOB,∠OAB=90°,直角边AO在x轴上,且AO=1,将Rt△AOB绕原点O顺时针旋转90°后,再将各边长扩大一倍,得到等腰直角三角形A1OB1;将Rt△A1OB1绕原点O顺时针转90°后,再将各边长扩大一倍,得到等腰三角形A2OB2......依此规律,得到等腰直角三角形A2017OB2017,则点B2017的坐标_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这是一个古老的传说,讲一个犯人利用概率来增加他得到宽恕的机会.给他两个碗,一个里面装着5个黑球,另一个里面装着除颜色不同外其它都一样的5个白球.把他的眼睛蒙着,然后要选择一个碗,并从里面拿出一个球,如果他拿的是黑球就要继续关在监狱里面,如果他拿的是白球,就将获得自由.在蒙住眼睛之前允许他把球混合,重新分装在两个碗内(两个碗球数可以不同).你能设想一下这个犯人怎么做,使得自己获得自由的机会最大?则犯人获得自由的最大机会是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com