
【题目】对实数a,b定义新运算“![]() ”
” 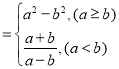
例如:![]()
(1)化简![]() _________.
_________.
(2)化简![]() _________.
_________.
(3)化简![]() .
.
【答案】(1)![]() (2)-1(3)x≥4, 8x236x+16;x<4,
(2)-1(3)x≥4, 8x236x+16;x<4,![]() .
.
【解析】
(1)先判断x+1与x的大小,再选择套用的运算;
(2)利用完全平方公式,判断0与(x2+4x+9)的大小,再选择合适的新定义运算,计算即可;
(3)不能判断代数式(3x5)与(x+3)的大小,需分类套用新定义运算的公式进行计算.
(1)因为x+1>x,
所以:(x+1)![]() x=(x+1)2x2
x=(x+1)2x2
=2x+1
故答案为:2x+1
(2)因为x2+4x+9=(x+2)2+5>0,
所以:0![]() (x2+4x+9)=
(x2+4x+9)=![]() =1;
=1;
(3)当(3x5)≥(x+3),即x≥4时.
(3x5)![]() (x+3)
(x+3)
=(3x5)2(x+3)2
=8x236x+16;
当(3x5)<(x+3),即x<4时.
(3x5)![]() (x+3)
(x+3)
=![]()
=![]()
=![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角∠α与∠β满足2α+β=90°,那么,我们将这样的三角形称为“准互余三角形”.在△ABC中,已知∠C=90°,BC=3,AC=4(如图所示),点D在AC边上,联结BD.如果△ABD为“准互余三角形”,那么线段AD的长为_____(写出一个答案即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
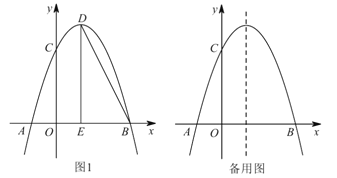
(1)求此抛物线的解析式;
(2)点![]() 是抛物线上的动点,设点
是抛物线上的动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,
,![]() ,将
,将![]() 沿着
沿着![]() 翻折,得
翻折,得![]() ,若四边形
,若四边形![]() 恰好为正方形,直接写出
恰好为正方形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 与
与![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求抛物线的解析式;
(2)如图1,点![]() 是抛物线上(
是抛物线上(![]() 轴下方)的一个动点,过点
轴下方)的一个动点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() 试判断在点
试判断在点![]() 运动过程中,以点
运动过程中,以点![]() 为顶点的四边形能否构成平行四边形,若能,请求出点
为顶点的四边形能否构成平行四边形,若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
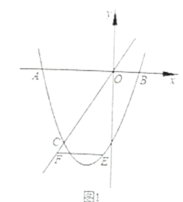
(3)如图2,点![]() 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() 当点
当点![]() 在抛物线上
在抛物线上![]() 之间运动时,连接
之间运动时,连接![]() 交
交![]() 于点
于点![]() 连接
连接![]() 并延长交
并延长交![]() 于点
于点![]() 猜想在点
猜想在点![]() 的运动过程中,
的运动过程中,![]() 的和是否为定值?若是,试求出该定值;若不是,请说明理由.
的和是否为定值?若是,试求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
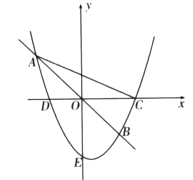
【题目】定义:若抛物线![]() 上有两点
上有两点![]() 关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若抛物线![]() 是“完美抛物线”,求
是“完美抛物线”,求![]() 的值;
的值;
(3)若完美抛物线![]() 与
与![]() 轴交于点E与
轴交于点E与![]() 轴交于
轴交于![]() 两点(点D在点C的左侧),顶点为点
两点(点D在点C的左侧),顶点为点![]() ,
,![]() 是以
是以![]() 为直角边的直角三角形,点
为直角边的直角三角形,点![]() ,求点
,求点![]() 中
中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
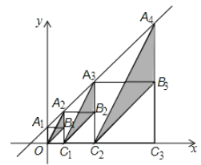
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,如图,作正方形
,如图,作正方形![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 轴上,将图中阴影部分三角形的面积从左到右依次记为
轴上,将图中阴影部分三角形的面积从左到右依次记为![]() ,则
,则
(1)![]() 的值为___________;
的值为___________;
(2)![]() 的值为___________.(含
的值为___________.(含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
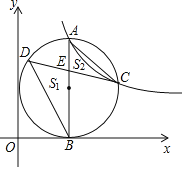
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com