
分析 把a+$\frac{1}{a}$=1+$\sqrt{10}$两边平方,根据完全平方公式展开,即可解答.
解答 解:∵$a+\frac{1}{a}=1+\sqrt{10}$
∴$(a+\frac{1}{a})^{2}=(1+\sqrt{10})^{2}$,
${a}^{2}+2+\frac{1}{{a}^{2}}=1+2\sqrt{10}+10$,
${a}^{2}+\frac{1}{{a}^{2}}=9+2\sqrt{10}$,
$(a-\frac{1}{a})^{2}={a}^{2}-2+\frac{1}{{a}^{2}}=9+2\sqrt{10}-2$=7+2$\sqrt{10}$.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程mx2-(m+1)x+1=0
已知关于x的一元二次方程mx2-(m+1)x+1=0查看答案和解析>>
科目:初中数学 来源: 题型:选择题
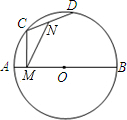 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )| A. | 随C、D的运动位置而变化,且最大值为4 | |
| B. | 随C、D的运动位置而变化,且最小值为2 | |
| C. | 随C、D的运动位置长度保持不变,等于2 | |
| D. | 随C、D的运动位置而变化,没有最值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com