
 如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.
如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.分析 (1)当t秒QB=2PB时,BP=6-2t,BQ=8-t,就有8-t=2(6-2t),求出结论就可以了;
(2)由(1)求出t的值就可以求出BP、BQ的值,根据矩形的面积减去三角形BPQ的面积就可以求出结论.
解答 解:(1)由题意可知AP=2t,CQ=t,
∴PB=AB-AP=6-2t,QB=CB-CQ=8-t.
当QB=2PB时,有8-t=2(6-2t).
解这个方程,得t=$\frac{4}{3}$,
所以当t=$\frac{4}{3}$秒时,QB=2PB.
(2)当t=$\frac{4}{3}$时,PB=6-2t=$\frac{10}{3}$,QB=8-t=$\frac{20}{3}$,
∴S$△QPB=\frac{1}{2}$PQ•QB=$\frac{1}{2}×\frac{10}{3}×\frac{20}{3}$=$\frac{100}{9}$,
∵S长方形ABCD=AB•CB=6×8=48,
∴S阴影=S长方形ABCD-S△QPB=$\frac{332}{9}$.
点评 本题考查了动点问题的函数图象,运用一元一次方程解实际问题,三角形的面积公式,矩形的面积公式,解答时求出t的值是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
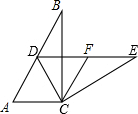 如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=α,将△ABC绕点C按顺时针方向旋转β后得到△DEC,点D恰好落在AB边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
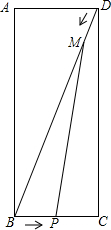 如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.
如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<$\frac{9}{4}$ | B. | m>-$\frac{9}{4}$ | C. | m>$\frac{9}{4}$ | D. | m<-$\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com