
����Ŀ����ͼ����֪�ھ���ABCD�У�AD��8��CD��4����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B��E��F���㹲��ʱ������ͬʱֹͣ�˶������E�ƶ���ʱ��Ϊt���룩��
��1����tΪ��ֵʱ������ͬʱֹͣ�˶���
��2�����ı���BCFE�����ΪS����S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3����tΪ��ֵʱ����E��F��C����Ϊ������������ǵ��������Σ�
��4����tΪ��ֵʱ����BEC����BFC��

���𰸡���1����t��4ʱ������ͬʱֹͣ�˶�����2��![]() ����
����![]() ����
����
��3����t��ֵΪ4��![]() ��
��![]() ʱ����E��F��C����Ϊ������������ǵ��������Σ�
ʱ����E��F��C����Ϊ������������ǵ��������Σ�
��4����t��![]() ʱ����BEC����BFC��
ʱ����BEC����BFC��
��������
��1������������ɵõ�B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ʱ�ɵõ�����FED�ס�FBC��ͬʱ��Ӧ�ı߶�������t��ʾ���õ�![]() �����t���ɣ�
�����t���ɣ�
��2���ı���BCFE�����=������BCE�����+������EFC�������ͨ�������ED��t��CF��2t�����ɱ�ʾ��S��t�ĺ�����ϵ��
��3����E��F��C����Ϊ������������ǵ��������Σ�����Ҫ��������������˭Ϊ�ף�˭Ϊ�ߣ�����EF��ECʱ�����Fֻ����CD���ӳ����ϣ�����EC��FCʱ������EF��FCʱ���ٷֱ��ú�t��ʽ�ӱ�ʾ����Ӧ�ߵ�ƽ������ü��ɡ���ע��ȡ�ᣩ
��4��������ã���Rt��BCF��Rt��CDE�У��ߡ�BCF����CDE��90����![]() Rt��BCF��Rt��CDE����BCE����CED������BEC����BFC�����BEC����BCE����BE��BC=8��
Rt��BCF��Rt��CDE����BCE����CED������BEC����BFC�����BEC����BCE����BE��BC=8��![]() ����
����![]() ���������t��ֵ����ע��ȡ�ᣩ
���������t��ֵ����ע��ȡ�ᣩ
�⣺��1����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ͼ��ʾ��
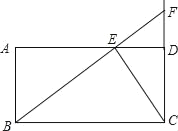
�������֪��ED��t��BC��8��FD��2t��4��FC��2t��
��ED��BC��
���FED�ס�FBC��
��![]() ��
��
��![]() ��
��
���t��4��
�൱t��4ʱ������ͬʱֹͣ�˶���
��2����ED��t��CF��2t��
��![]() ��
��
��![]() ����
����![]() ����
����
��3������EF��ECʱ�����Fֻ����CD���ӳ����ϣ�
��![]() ��
��
![]() ��
��
��![]() ��
��
��t��4��t��0����ȥ����
����EC��FCʱ��
��![]() ��
��![]() ��
��
��![]()
��![]() ��
��
����EF��FCʱ��
��![]() ��
��![]() ��
��
��![]() ��
��
��t1��![]() ����ȥ����t2��
����ȥ����t2��![]() ��
��
�൱t��ֵΪ4��![]() ��
��![]() ʱ����E��F��C����Ϊ������������ǵ��������Σ�
ʱ����E��F��C����Ϊ������������ǵ��������Σ�
��4����Rt��BCF��Rt��CDE��
�ߡ�BCF����CDE��90����![]() ��
��
��Rt��BCF��Rt��CDE��
���BFC����CED��
��AD��BC��
���BCE����CED��
����BEC����BFC�����BEC����BCE��
��BE��BC��
��![]() ��
��
��![]() ��
��
��t1��![]() ����ȥ����t2��
����ȥ����t2��![]() ��
��
�൱t��![]() ʱ����BEC����BFC��
ʱ����BEC����BFC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±�ͳ�Ƶ��Ǽס��������������������������ͳ�Ʊ����������²�������ͳ��ͼ��
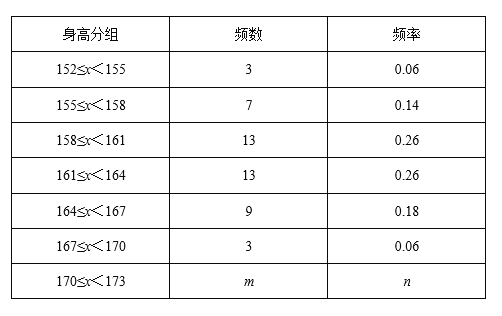
��������ͳ�Ʊ�����������⣺
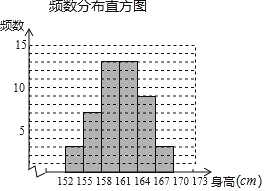
��1��ͳ�Ʊ��е�m���� ����n���� ��������Ƶ���ֲ�ֱ��ͼ����������
��2������β����������������ߵ���λ������ ����Χ�ڣ�
��3�������߲�����167cm�������У��װ���2�ˣ��ִ���Щ���߲�����167cm�������������ѡ2�˲��䵽ѧУ���커�����У������б�����״ͼ�ķ�����������˶�������ͬ�༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
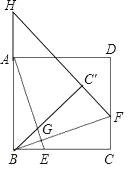
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ���BE��CF������AE��BF�����ཻ�ڵ�G������BCF��BF���۵õ���BC��F���ӳ�FC�佻BA�ӳ����ڵ�H��
��1������֤��AE��BF��
������AE��BF��λ�ù�ϵ����֤����Ľ��ۣ�
��2����AB��3��EC��2BE����BH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
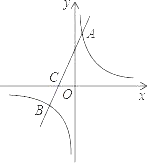
����Ŀ����ͼ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����2��0������A��������Ϊ6��AC��3CB��
��ͼ����A��B���㣬��x�ύ�ڵ�C����2��0������A��������Ϊ6��AC��3CB��
��1�����������Ľ���ʽ��
��2����ֱ��д������ʽ��![]() ��kx+b��4�Ľ⼯��
��kx+b��4�Ľ⼯��
��3����P��x��y����ֱ��y��k+b�ϵ�һ�����㣬�����㣨2���еIJ���ʽ�飬����P��PQ��y�ύy���ڵ�Q������BPQ�������ΪS����S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
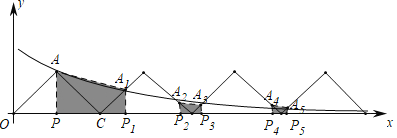
����Ŀ����ͼ���ڡ�AOC�У���OAC��90����AO��AC��OC��2������AOC������ƽ��ֱ������ϵ�У���O������ԭ���غϣ�б��OC��x���ϣ�����������y��![]() ��x��0����ͼ����A������AOC��x������ƽ��2����λ���ȣ���ƽ�ƺ������εı��뷴��������ͼ��Ľ���ΪA1��A2���ظ�ƽ�Ʋ��������μǽ���ΪA3��A4��A5��A6���ֱ����A��A1��A2��A3��A4��A5����x��Ĵ��ߣ��������μ�ΪP��P1��P2��P3��P4��P5�����ı���APP1A1�������ΪS1���ı���A2P2P3A3�������ΪS2������Sn��_____�����ú�n�Ĵ���ʽ��ʾ��nΪ��������
��x��0����ͼ����A������AOC��x������ƽ��2����λ���ȣ���ƽ�ƺ������εı��뷴��������ͼ��Ľ���ΪA1��A2���ظ�ƽ�Ʋ��������μǽ���ΪA3��A4��A5��A6���ֱ����A��A1��A2��A3��A4��A5����x��Ĵ��ߣ��������μ�ΪP��P1��P2��P3��P4��P5�����ı���APP1A1�������ΪS1���ı���A2P2P3A3�������ΪS2������Sn��_____�����ú�n�Ĵ���ʽ��ʾ��nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
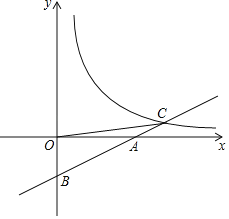
����Ŀ����ͼ��ֱ��y��ax+b��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0����2�����뷴��������y��![]() ��x��0����ͼ���ڵ�C��6��m����
��x��0����ͼ���ڵ�C��6��m����
��1����ֱ�ߺͷ����������ı���ʽ��
��2������OC����x������һ��P��ʹ��OPC����OCΪ���ĵ��������Σ��������P�����ꣻ
��3�����ͼ����ֱ��д������ʽ![]() ��ax+b�Ľ⼯��
��ax+b�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ѧУ���������ɱʴ��ͱʼDZ���Ϊʫ�����д�����ʤѧ���Ľ�Ʒ�����Ļ��̳�����2���ʴ���1���ʼDZ��軨25Ԫ������3���ʴ���2���ʼDZ��軨40Ԫ
��1����ʴ��ͱʼDZ��ĵ��۸��Ƕ���Ԫ��
��2����֪ѧУ������ʴ��ͱʼDZ���180���Ļ��̳��涨һ���Թ��ﳬ��500Ԫ������500Ԫ�IJ��ְ������շѣ�ѧУ�˴ι���Ʒ�ķ��ò�����1000Ԫ������֪ѧУ����ܹ�����ٸ��ʴ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
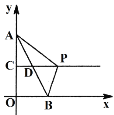
����Ŀ����ͼ����A��0��4����B��2��0������C��D�ֱ���OA��AB���е㣬������CD����һ����P������ABP��ֱ�������Σ����P������Ϊ_____.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com