
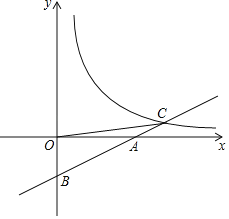
【题目】如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y=![]() (x>0)的图象交于点C(6,m).
(x>0)的图象交于点C(6,m).
(1)求直线和反比例函数的表达式;
(2)连接OC,在x轴上找一点P,使△OPC是以OC为腰的等腰三角形,请求出点P的坐标;
(3)结合图象,请直接写出不等式![]() ≥ax+b的解集.
≥ax+b的解集.
【答案】(1)y=![]() x﹣2;y=
x﹣2;y=![]() ;(2)点P1的坐标为(
;(2)点P1的坐标为(![]() ,0),点P2的坐标为(﹣
,0),点P2的坐标为(﹣![]() ,0),(12,0);(3)0<x≤6
,0),(12,0);(3)0<x≤6
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出直线AB的函数表达式,利用一次函数图象上点的坐标特征可得出点C的坐标,由点C的坐标,利用待定系数法即可求出反比例函数的表达式;
(2)过点C作CD⊥x轴,垂足为D点,利用勾股定理看求出OC的长,分OC=OP和CO=CP两种情况考虑:①当OP=OC时,由OC的长可得出OP的长,进而可求出点P的坐标;②当CO=CP时,利用等腰三角形的性质可得出OD=PD,结合OD的长可得出OP的长,进而可得出点P的坐标;
(3)观察图形,由两函数图象的上下位置关系,即可求出不等式![]() ≥ax+b的解集.
≥ax+b的解集.
解:(1)将A(4,0),B(0,﹣2)代入y=ax+b,得:
![]() ,解得:
,解得: ,
,
∴直线AB的函数表达式为y=![]() x﹣2.
x﹣2.
当x=6时,y=![]() x﹣2=1,
x﹣2=1,
∴点C的坐标为(6,1).
将C(6,1)代入y=![]() ,得:1=
,得:1=![]() ,
,
解得:k=6,
∴反比例函数的表达式为y=![]() .
.
(2)过点C作CD⊥x轴,垂足为D点,则OD=6,CD=1,
∴OC=![]() .
.
∵OC为腰,
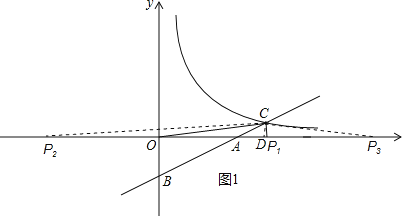
∴分两种情况考虑,如图1所示:
①当OP=OC时,∵OC=![]() ,
,
∴OP=![]() ,
,
∴点P1的坐标为(![]() ,0),点P2的坐标为(﹣
,0),点P2的坐标为(﹣![]() ,0);
,0);
②当CO=CP时,DP=DO=6,
∴OP=2OD=12,
∴点P3的坐标为(12,0).
(3)观察函数图象,可知:当0<x<6时,反比例函数y=![]() 的图象在直线y=
的图象在直线y=![]() x﹣2的上方,
x﹣2的上方,
∴不等式![]() ≥ax+b的解集为0<x≤6.
≥ax+b的解集为0<x≤6.


科目:初中数学 来源: 题型:
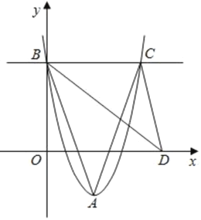
【题目】如图,在平面直角坐标系中,点A是抛物线y=ax2+bx+c的顶点,点B(0,2)是抛物线与y轴的交点,直线BC平行于x轴,交抛物线于点C,D为x轴上任意一点,若S△ABC=3,S△BCD=2,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点M从点A出发,沿A→B→C方向运动,当点M到达点C时停止运动,过点M作MN⊥AM交CD于点N,设点M的运动路程为x,CN=y,图2表示的是y与x的函数关系的大致图象,则矩形ABCD的面积是( )
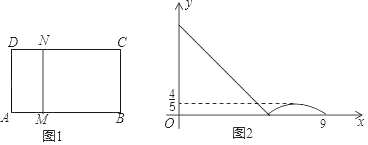
A.20B.18C.10D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
(1)求当t为何值时,两点同时停止运动;
(2)设四边形BCFE的面积为S,求S与t之间的函数关系式,并写出t的取值范围;
(3)求当t为何值时,以E,F,C三点为顶点的三角形是等腰三角形;
(4)求当t为何值时,∠BEC=∠BFC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十三五”以来,党中央,国务院不断加大脱贫攻坚的支持决策力度,并出台配套文件,国家机关各部门也出台多项政策文件或实施方案.某单位认真分析被帮扶人各种情况后,建议被帮扶人大力推进特色产业,大量栽种甜橙;同时搭建电商运营服务平台,开设网店销售农产品橙.丰收后,将一批甜橙采取现场销售和网络销售相结合进行试销,统计后发现:同样多的甜橙,现场销售可获利800元,网络销售则可获利1000元,网络销售比现场销售每件多获利5元
(1)现场销售和网络销售每件分别多少元?
(2)根据甜橙试销情况分析,现场销售量a(件)和网络销售量b(件)满足如下关系式:b=﹣![]() a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() 两城市间修建一条高速铁路(即线段
两城市间修建一条高速铁路(即线段![]() ),经测量,森林保护区的中心
),经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
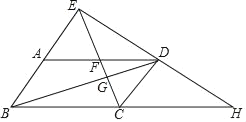
【题目】如图,四边形ABCD是平行四边形,连接BD,点E在BA的延长线上,连接EC,分别交AD、BD于点F、点G,连接ED并延长交BC的延长线于点H,则下列结论错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学九年级学生中考体育成绩情况,现从中抽取部分学生的体育成绩进行分段(A:50分、B:49~40分、C:39~30分、D:29~0分)统计,统计结果如图1、图2所示.
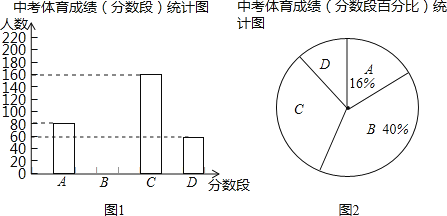
根据上面提供的信息,回答下列问题:
(1)本次抽查了 名学生的体育成绩;
(2)补全图1,求图2中D分数段所占的圆心角是 度;
(3)已知该校九年级共有900名学生,请估计该校九年级学生体育成绩达到40分以上(含40分)的人数为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
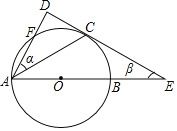
【题目】如图,已知⊙O的直径AB=10,AC是⊙O的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作AD⊥DE,垂足为D,与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β,且0°<α<45°.
(1)求β(用含α的代数式表示);
(2)连结OF交AC于点G,若AG=CG,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com