
分析 (1)首先利用待定系数法求得直线l1的解析式,然后直接把P点坐标代入可求出a的值;利用待定系数法确定L2得解析式;
(2)先确定A点坐标,然后根据三角形面积公式计算.
解答 解:(1)∵直线l1经过(2,3)和(-1,-3),
∴$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴直线l1的解析式为:y=2x-1,
把P(-2,a)代入y=2x-1得:a=2×(-2)-1=-5;
设L2的解析式为y=kx,
把P(-2,-5)代入得-5=-2k,解得k=$\frac{5}{2}$,
所以L2的解析式为y=$\frac{5}{2}$x;
(2)对于y=2x-1,令x=0,
解得y=-1,
则A点坐标为(0,-1),
所以S△APO=$\frac{1}{2}$×2×1=1.
点评 此题考查两条直线的交点问题,待定系数法求函数解析式,三角形的面积,掌握待定系数法求函数解析式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
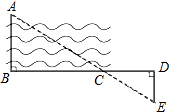 如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?
如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
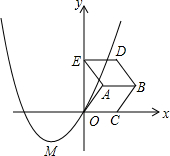 如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.
如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
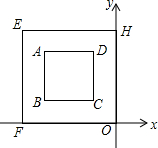 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )| A. | (-2,2) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-4,4) | D. | (0,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{128}$ | D. | $\frac{1}{256}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
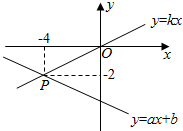 如图,已知直线y=ax+b和直线y=kx交于点P(-4,-2),则关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
如图,已知直线y=ax+b和直线y=kx交于点P(-4,-2),则关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com