
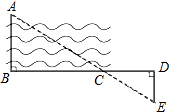
 如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?
如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
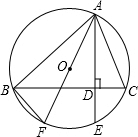 如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.
如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
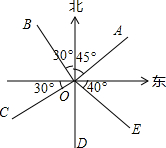 如图.根据点A、B、C、D、E在图中的位置填空.
如图.根据点A、B、C、D、E在图中的位置填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
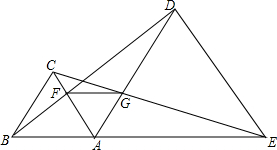 如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.
如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com