
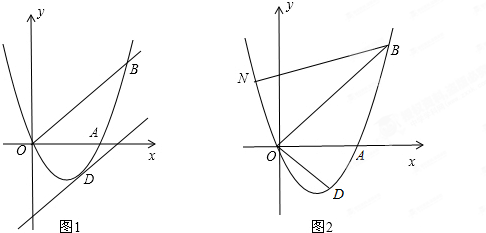
分析 (1)利用待定系数法求二次函数解析式进而得出答案即可;
(2)根据已知条件可求出OB的解析式为y=x,则向下平移m个单位长度后的解析式为:y=x-m.由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标;
(3)设点N(n,$\frac{1}{4}$n+3),又点N在抛物线y=x2-3x上,代入抛物线的解析式即可求出n的值,进而得到N的坐标;
解答 解:(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)
∴将A与B两点坐标代入得:$\left\{\begin{array}{l}{9a+3b=0}\\{16a+4b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$.
∴抛物线的解析式是y=x2-3x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,
解得:k1=1.
∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=x-m,
∵点D在抛物线y=x2-3x上,
∴可设D(x,x2-3x),
又∵点D在直线y=x-m上,
∴x2-3x=x-m,即x2-4x+m=0,
∵抛物线与直线只有一个公共点,
∴△=16-4m=0,
解得:m=4,
此时x1=x2=2,y=x2-3x=-2,
∴D点的坐标为(2,-2).
(3)∵直线OB的解析式为y=x,且A(3,0),
∴点A关于直线OB的对称点A′的坐标是(0,3),
根据轴对称性质和三线合一性质得出∠A′BO=∠ABO,
设直线A′B的解析式为y=k2x+3,过点(4,4),
∴4k2+3=4,解得:k2=$\frac{1}{4}$,
∴直线A′B的解析式是y=$\frac{1}{4}$x+3,
∵∠NBO=∠ABO,∠A′BO=∠ABO,
∴BA′和BN重合,
即点N在直线A′B上,
∴设点N(n,$\frac{1}{4}$n+3),又点N在抛物线y=x2-3x上,
∴$\frac{1}{4}$=n2-3n,
解得:n1=-$\frac{3}{4}$,n2=4(不合题意,舍去)
∴N点的坐标为(-$\frac{3}{4}$,$\frac{45}{16}$).
点评 本题是基于二次函数的代数几何综合题,综合考查了待定系数法求抛物线解析式、一次函数(直线)的平移、一元二次方程根的判别式、翻折变换、旋转变换以及相似三角形等重要知识点.本题将初中阶段重点代数、几何知识熔于一炉,难度很大,对学生能力要求极高,具有良好的区分度,是一道非常好的中考压轴题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
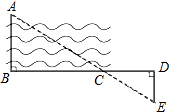 如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?
如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )| A. | 2秒 | B. | 6秒 | C. | 2秒或6秒 | D. | 4秒或8秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
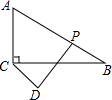 如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.
如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{128}$ | D. | $\frac{1}{256}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com