
 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )| A. | 2秒 | B. | 6秒 | C. | 2秒或6秒 | D. | 4秒或8秒 |
分析 分为两种情况:①当M、N分别在OA、OC上时,可证明△OMN∽△OAC,由题意可求得OM的长,即可求得t的值;
②当M、N分别在AB、BC上时,可证明△BMN∽△BAC,由题意可求得BM的长,即可由相似三角形的性质求得t的值,综合以上两种情况即是要求的t值.
解答 解: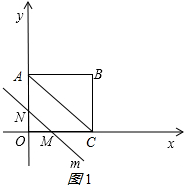 x轴正方向以每秒1个单位长度的速度运动,
x轴正方向以每秒1个单位长度的速度运动,
设直线m运动的时间为t秒,
分为两种情况:
①当M、N分别在OA、OC上时,如图1所示:
∵直线m平行于对角线AC
∴△OMN∽△OAC,
∴$\frac{MN}{AC}=\frac{OM}{OC}$=$\frac{t}{4}$=$\frac{1}{2}$,
解得:t=2;
②当M、N分别在AB、BC上时,如图2所示:
∵直线m平行于对角线AC
∴△BMN∽△BAC,
∴$\frac{MN}{AC}$=$\frac{BM}{BC}$=$\frac{t-4}{4}$=$\frac{1}{2}$,
解得:t=6.
综上所述,当t=2秒或6秒时,MN=$\frac{1}{2}$AC;
故选:C.
点评 本题考查了相似三角形的判定和性质、三角形中位线定理;证明三角形相似得出比例式是解决问题的关键;注意分类讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
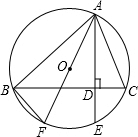 如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.
如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
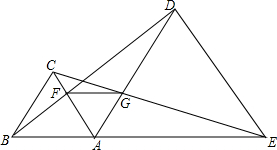 如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.
如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 浙江卫视六频道《我老爸最棒》栏目中有一项“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为$\frac{1}{6}$.
浙江卫视六频道《我老爸最棒》栏目中有一项“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为$\frac{1}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com