
【题目】 某单位需要购买一些钢笔和笔记本.若购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.
(1)求买一支钢笔要多少钱?
(2)若购买了钢笔和笔记本共50件,付款可能是810元吗?说明理由.
【答案】(1)16;(2)不可能,理由见解析.
【解析】
(1)设一支钢笔x元,一本笔记本y元,根据“购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设学校购买m支钢笔,则购买(50﹣m)本笔记本,根据总价=单价×数量结合购买的费用为810元,即可得出关于m的一元一次方程,解得m的值为不大于50的正整数即可.
解:(1)设一支钢笔x元,一本笔记本y元,
根据题意得:![]() ,
,
解得:![]() .
.
答:一支钢笔16元,一本笔记本10元.
(2)设学校购买m支钢笔,则购买(50﹣m)本笔记本,
根据题意得:16m+10(50﹣m)=810,
解得:m=52>50,不符合题意.
答:若购买了钢笔和笔记本共50件,付款不可能是810元.


科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PB=4,PC=4![]() ,则线段AB的长为_____.
,则线段AB的长为_____.
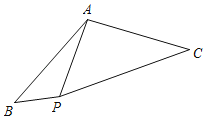
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.
(1)求证:CD⊥CG;
(2)若tan∠MEN=![]() ,求
,求![]() 的值;
的值;
(3)已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为![]() ?请说明理由.
?请说明理由.
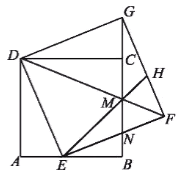
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
由上表结果,计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________.当试验组数增加到很大时,请你对这三种结果的可能性的大小作出预测:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O于点E,连接BE、CE.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,EF=4,DE的长为 .
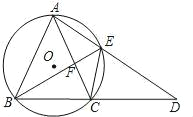
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征.在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“纯数”.定义;对于自然数n,在计算n+(n+1)+(n+2)时,各数位都不产生进位,则称这个自然数n为“数”,例如:32是”纯数”,因为计算32+33+34时,各数位都不产生进位;23不是“纯数”,因为计算23+24+25时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com