
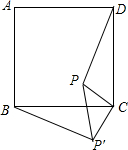
 如图,P是正方形ABCD内一点,将△PCD绕点C逆时针方向旋转后与△P′CB重合,若PC=1,则PP′=$\sqrt{2}$.
如图,P是正方形ABCD内一点,将△PCD绕点C逆时针方向旋转后与△P′CB重合,若PC=1,则PP′=$\sqrt{2}$. 分析 根据正方形的性质得CD=CB,∠BCD=90°,再根据旋转的性质得CP=CP′,∠PCP′=∠DCB=90°,则可判断△PCP′为等腰直角三角形,于是PP′=$\sqrt{2}$CP=$\sqrt{2}$.
解答 解:∵四边形ABCD为正方形,
∴CD=CB,∠BCD=90°,
∵△PCD绕点C逆时针方向旋转后与△P′CB重合,
∴CP=CP′,∠PCP′=∠DCB=90°,
∴△PCP′为等腰直角三角形,
∴PP′=$\sqrt{2}$CP=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
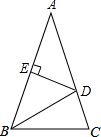 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
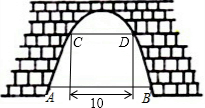 如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.
如图是一座抛物线拱形桥,在正常水位时,水面AB宽是20m,水位上升3m就达到警戒线CD,这是水面宽度为10m,请构建适当的水平直角坐标系求抛物线所对应的函数表达式,并求水位到达警戒线时拱顶与水面之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com