
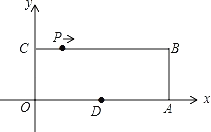
【题目】如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,
A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)直接写出坐标:D( , );
(2)当四边形PODB是平行四边形时,求t的值;
(3)在平面直角坐标系内是否存在点Q,使得以O、P、D、Q为顶点四边形为菱形,若存在,请直接写出Q点坐标;若不存在,请说明理由.
【答案】(1)5,0;(2)t=5;(3)满足条件的点Q的坐标为:(8,4)、(﹣3,4)、(3,4)、(2.5,﹣4).
【解析】
(1)根据中点的定义求出OD的长即可解决问题;
(2)利用平行四边形的性质求出PC=5即可解决问题;
(3)分四种情形:当P1O=OD=5或P2O=P2D或P3D=OD=5或P4D=OD=5时,分别求解即可.
解:(1)∵A(10,0),OD=DA,
∴OA=10,OD=DA=5,
∴D(5,0).
故答案为5,0.
(2)∵四边形 PODB 是平行四边形,
∴PB=OD=5,
∴PC=5,
∴t=5.
(3)当P1O=OD=5时,由勾股定理可以求得P1C=3,可得Q1(8,4)
当P2O=P2D时,作P2E⊥OA,
∴OE=ED=2.5,可得Q2(2.5,﹣4),
当P3D=OD=5时,作DF⊥BC,由勾股定理,得P3F=3,
∴P3C=2,可得Q3(﹣3,4),
当P4D=OD=5时,作P4G⊥OA,由勾股定理,得DG=3,
∴OG=8,可得Q4(3,4),

综上所述,满足条件的点Q的坐标为:(8,4)、(﹣3,4)、(3,4)、(2.5,﹣4).


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,其中有这样一道名题:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几步及之?”意思是说:走路快的人走100步的时候,走路慢的才走了60步,走路慢的人先走100步,然后走路快的人去追赶,问走路快的人要走多少部才能追上?若设走路快的人要走x步才能追上走路慢的人,此时走路慢的人又走了y步,根据题意可列方程组为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批排球和足球,已知购买2个排球和1个足球共需321元,购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价;
(2)若学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
求1+2+22+23+…...+22014的值,另S=1+2+22+23+…...+22014,
等式两边同时乘2,得2S=2+22+23+.......+22014+22015
两式相减,得2S - S = 22015 -1 所以S = 22015 - 1
依据以上计算方法,计算:1 + 3 + 32 + ..... + 32019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市有5 000万人口,若平均每3.3人为一个家庭,平均每个家庭每周丢弃5个塑料袋,一年将丢弃多少个塑料袋?若每1 000个塑料袋污染1平方米土地,那么该城市一年被塑料袋污染的土地是多少?(保留2个有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
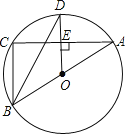
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com