
【题目】某校计划购买一批排球和足球,已知购买2个排球和1个足球共需321元,购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价;
(2)若学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买足球多少个?
【答案】(1)每个排球和每个足球的售价分别为102元,117元;(2)最多可购买26个足球.
【解析】
(1)设每个排球和每个足球的售价分别为x元,y元,根据题意列出方程组,求出方程组的解即可;
(2)设排球购买a个,则足球购买(50-a)个,根据题意列出不等式,求出不等式的解集即可确定出最多购买的足球.
解:(1)设每个排球和每个足球的售价分别为x元,y元,
根据题意得:![]() ;
;
解得:![]() ;
;
则每个排球和每个足球的售价分别为102元,117元;
(2)设足球购买a个,则排球购买(50-a)个,
根据题意得:117a+102(50-a)≤5500,
整理得:15a≤400,
解得:a≤26![]() ,
,
则最多可购买26个足球.


科目:初中数学 来源: 题型:
【题目】网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网两种收费方式,用户可以任选其一:A:计时制:0.05元/分;B:全月制:54元/月(限一部个人住宅电话入网).此外B种上网方式要加收通信费0.02元/分.
①某用户某月上网的时间为x小时,两种收费方式的费用分别为![]() (元)、
(元)、![]() (元),写出
(元),写出![]() 、
、![]() 与x之间的函数关系式.
与x之间的函数关系式.
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=2;
③![]() ;④b<1.其中正确的结论个数是( )
;④b<1.其中正确的结论个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车在相距70千米的甲、乙两地往返行驶,由于行程中有一坡度均匀的小山,该汽车由甲地到乙地需用2小时30分,而从乙地到甲地需用2小时18分.若汽车在平地上的速度为30千米/时,上坡的速度为20千米/时,下坡的速度为40千米/时,求从甲地到乙地的行程中,平路、上坡路、下坡路各多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).

(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,对角线AC和BD相交于点O,正方形A1B1C1O的边OA1交AB于点E,OC1交BC于点F,正方形A1B1C1O绕O点转动的过程中,与正方形ABCD重叠部分的面积为_____(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
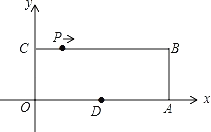
【题目】如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,
A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)直接写出坐标:D( , );
(2)当四边形PODB是平行四边形时,求t的值;
(3)在平面直角坐标系内是否存在点Q,使得以O、P、D、Q为顶点四边形为菱形,若存在,请直接写出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com