
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0),点B(3,0)和点C(0,3).

(1)求抛物线的解析式和顶点E的坐标;
(2)点C是否在以BE为直径的圆上?请说明理由;
(3)点Q是抛物线对称轴上一动点,点R是抛物线上一动点,是否存在点Q、R,使以Q、R、C、B为顶点的四边形是平行四边形?若存在,直接写出点Q、R的坐标,若不存在,请说明理由.
【答案】(1)y=-x2+2x+3,E (1,4);(2)在;(3)Q1(1,-2),R1(4,-5);
Q2(1,-8),R2(-2,-5);R3(2,3),Q3(1,0).
【解析】试题分析:(1)运用待定系数法即可得出函数关系式,然后进行配方即可得出顶点坐标;
(2)过点E分别作x轴、y轴的垂线,垂足分别F、G.易证△BCE为直角三角形,点C在以BE为直径的圆上;
(3)利用平行四边形的性质易得点Q、R的坐标.
试题解析: (1) 将A(-1,0),B(3,0)和C(0,3)代入y=ax2+bx+c
得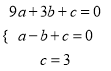
解得
∴抛物线的解析式为y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点E的坐标为(1,4).
(2)点C在以BE为直径的圆上,理由如下:
如图,过点E分别作x轴、y轴的垂线,垂足分别F、G.
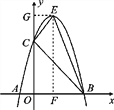
在Rt△BOC中,OB=3,OC=3,∴BC2=18
在Rt△CEG中,EG=1,CG=OG-OC=4-3=1,∴CE2=2
在Rt△BFE中,FE=4,BF=OB-OF=3-1=2, ∴BE2=20
∴BC2+CE2=BE2
故△BCE为直角三角形,点C在以BE为直径的圆上.
(3)存在,点Q、R的坐标分别为Q1(1,-2),R1(4,-5);
Q2(1,-8),R2(-2,-5);R3(2,3),Q3(1,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九(1)班的2名男生1名女生、九(2)的1名男生1名女生共5人中选出2名主持人.
(1)用树形图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A坐标为(4,4),点B的坐标为(2,0).
(1)求线段AB的长;
(2)点M是坐标轴上的一个点,若以AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;
(3)如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OCOD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要求写解题过程).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批排球和足球,已知购买2个排球和1个足球共需321元,购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价;
(2)若学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标为______ ;(2)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市有5 000万人口,若平均每3.3人为一个家庭,平均每个家庭每周丢弃5个塑料袋,一年将丢弃多少个塑料袋?若每1 000个塑料袋污染1平方米土地,那么该城市一年被塑料袋污染的土地是多少?(保留2个有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在疫情期间的复学准备工作中,为了贯彻落实“生命重于泰山,安全至关重要”的思想,计划购买室内、室外两种型号的消毒液.已知每桶室外消毒液的价格比每桶室内消毒液的价格多30元,买2桶室内消毒液和3桶室外消毒液共需340元.
(1)求室内、室外两种型号消毒液每桶的价格;
(2)根据学校实际情况,需购买室内、室外两种型号的消毒液共200桶,总费用不高于1.4万元,问室内消毒液至少要购买多少桶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com