
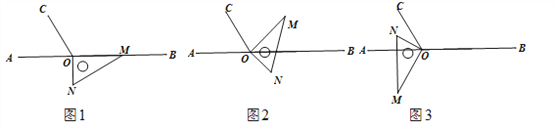
����Ŀ����ͼ1����OΪֱ��AB��һ��������O������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB������һ��ON��ֱ��AB���·���
��1����ͼ2����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ʹ��OM����BOC���ڲ�����OMǡ��ƽ����BOC����ʱ��AOM=_______����
��2����ͼ3��������ͼ2�е����ǰ��Ƶ�O����ʱ�뷽����ת��ʹ��ON����AOC���ڲ���̽����AOM����NOC֮��������ϵ����˵�����������
��3����ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ�����ʱ�뷽����תһ��������ת�Ĺ���������ֱ��ONǡ��ƽ����AOC�����ʱ���ǰ��Ƶ�O��ת��ʱ���Ƕ����룿��ֱ��д���𰸼���������˵��������
���𰸡���1��120����2����AOM����NOC =30������3��6���24��
�������������������1������OMǡ��ƽ�֡�BOC���á�BOC�Ķ�������2�������BOM�Ķ��������������AOM�Ķ����Ƕ��٣�
��2�����ȸ��ݡ�AOM-��NOC=30������BOC=120���������A0C=60����Ȼ����ݡ�AON=90��-��AOM=60��-��NOC���жϳ���AOM���NOC֮������ʲô������ϵ���ɣ�
��3�����������ǰ��Ƶ�O��ת��ʱ����x�룬���ݡ�BOC=120�����ɵá�AOC=60������BON=��COD=30����Ȼ�������ת60��ʱONƽ�֡�AOC���ɵ�10x=60��10x=240���ݴ����x��ֵ�Ƕ��ټ��ɣ�
�����������1����OMǡ��ƽ�֡�BOC��
���BOM=120���2=60����
���AOM=180��-60��=120����
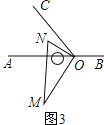
��2����ͼ3��
 ��
��
��AOM-��NOC=30����
�ߡ�BOC=120����
���A0C=60����
�ߡ�AON=90��-��AOM=60��-��NOC��
���AOM-��NOC=30����
��3�������ǰ��Ƶ�O��ת��ʱ����x�룬
�ߡ�BOC=120����
���AOC=60����
���BON=30����
����ת60��ʱONƽ�֡�AOC��
��10x=60��10x=240��
��x=6��x=24��
����ʱ���ǰ��Ƶ�O��ת��ʱ����6��24�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD����ֱ��BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��AD=8��AB=6����AE�ij��� 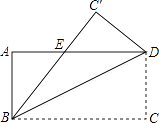
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ��
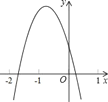
���н��ۣ���abc��0����2a��b��0����4a��2b+c��0������a+c��2��b2������ȷ�ĸ����У�������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ�����������Ŀ��
��1����ͼ����________��С�����壻
��2�� �������淽��ֽ�зֱ���������ͼ����ͼ��������ͼ����Ǧ��Ϳ����Ӱ����
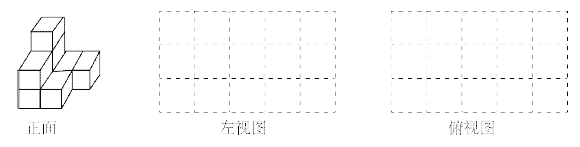
��3����С�������һ�������壬ʹ�����ĸ���ͼ������ͼ��������ͼ������������ͼһ�£��������ļ���������Ҫ________��С�����壬���Ҫ________��С������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ƶ�ʷֲ�ֱ��ͼ�У�����˵��������ǣ�������
A.ÿ��С�����ε��������Ƶ��
B.ÿ��С�����ε��������Ƶ��
C.Ƶ��=Ƶ������������
D.����С����������͵���1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ���������ʦͳ����ȫ��50��ͬѧ�ijɼ�������70�����µ�ռ12%��70��80�ֵ�ռ24%��80��90�ֵ�ռ36%������90�ּ�90�����ϵ��У��������ˣ�
A.13
B.14
C.15
D.28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ��ͬ����������ͼ��ʾ�Ĺ������ΰڷţ��۲�ÿ������ͼ���е������ĸ���������n������ͼ������245����������n=�� ��

A. 14 B. 15 C. 16 D. 17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���������( )
A. һ��ֱ������ֻ��һ������B. ��ֱ��ƽ�У�ͬ���ڽǻ���
C. һ���ǵ��ڲ���������D. �Զ�������ȵĽ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com