Question

【题目】菱形ABCD中，两条对角线AC，BD相交于点O，∠MON+∠BCD=180°，∠MON绕点O旋转，射线OM交边BC于点E，射线ON交边DC于点F，连接EF．

（1）如图1，当∠ABC=90°时，△OEF的形状是　　；

（2）如图2，当∠ABC=60°时，请判断△OEF的形状，并说明理由；

（3）在（1）的条件下，将∠MON的顶点移到AO的中点O′处，∠MO′N绕点O′旋转，仍满足∠MO′N+∠BCD=180°，射线O′M交直线BC于点E，射线O′N交直线CD于点F，当BC=4，且=时，直接写出线段CE的长．

Answer 1

【答案】（1）△OEF是等腰直角三角形（2）△OEF是等边三角形（3）线段CE的长为3+3或3﹣3

【解析】试题分析：（1）先求得四边形ABCD是正方形，然后根据正方形的性质可得∠EBO=∠FCO=45°，OB=OC，再根据同角的余角相等可得∠BOE=∠COF，然后利用“角边角”证明△BOE和△COF全等，根据全等三角形对应边相等即可得证；（2）过O点作OG⊥BC于G，作OH⊥CD于H，根据菱形的性质可得CA平分∠BCD，∠ABC+∠BCD=180°，求得OG=OH，∠BCD=180°-60°=120°，从而求得∠GOH=∠EOF=60°，再根据等量减等量可得∠EOG=∠FOH，然后利用“角边角”证明△EOG和△FOH全等，根据全等三角形对应边相等即可得证；（3）过O点作OG⊥BC于G，作OH⊥CD于H，先求得四边形O′GCH是正方形，从而求得GC=O′G=3，∠GO′H=90°，然后利用“角边角”证明△EO′G和△FO′H全等，根据全等三角形对应边相等即可证得△O′EF是等腰直角三角形，根据已知求得等腰直角三角形的直角边O′E的长，然后根据勾股定理求得EG，即可求得CE的长．

试题解析：（1）△OEF是等腰直角三角形；

证明：∵菱形ABCD中，∠ABC=90°，

∴四边形ABCD是正方形，

∴OB=OC，∠BOC=90°，∠BCD=90°，∠EBO=∠FCO=45°，

∴∠BOE+∠COE=90°，

∵∠MON+∠BCD=180°，

∴∠MON=90°，

∴∠COF+∠COE=90°，

∴∠BOE=∠COF，

在△BOE与△COF中，

，

∴△BOE≌△COF（ASA），

∴OE=OF，

∴△OEF是等腰直角三角形；

故答案为等腰直角三角形；

（2）△OEF是等边三角形；

证明：如图，

过O点作OG⊥BC于G，作OH⊥CD于H，

∴∠OGE=∠OGC=∠OHC=90°，

∵四边形ABCD是菱形，

∴CA平分∠BCD，∠ABC+BCD=180°，

∴OG=OH，∠BCD=180°﹣60°=120°，

∵∠GOH+∠OGC+∠BCD+∠OHC=360°，

∴∠GOH+∠BCD=180°，

∴∠MON+∠BCD=180°，

∴∠GOH=∠EOF=60°，

∵∠GOH=∠GOF+∠FOH，∠EOF=∠GOF+∠EOG，

∴∠EOG=∠FOH，

在△EOG与△FOH中，

，

∴△EOG≌△FOH（ASA），

∴OE=OF，

∴△OEF是等边三角形；

（3）证明：如图：

∵菱形ABCD中，∠ABC=90°，

∴四边形ABCD是正方形，

∴，

过O点作O′G⊥BC于G，作O′H⊥CD于H，

∴∠O′GC=∠O′HC=∠BCD=90°，

∴四边形O′GCH是矩形，

∴O′G∥AB，O′H∥AD，

∴，

∵AB=BC=CD=AD=4，

∴O′G=O′H=3，

∴四边形O′GCH是正方形，

∴GC=O′G=3，∠GO′H=90°

∵∠MO′N+∠BCD=180°，

∴∠EO′F=90°，

∴∠EO′F=∠GO′H=90°，

∵∠GO′H=∠GO′F+∠FO′H，∠EO′F=∠GO′F+∠EO′G，

∴∠EO′G=∠FO′H，

在△EO′G与△FO′H中，

，

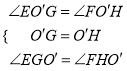∴△EO′G≌△FO′H（ASA），

∴O′E=O′F，

∴△O′EF是等腰直角三角形；

∵S正方形ABCD=4×4=16， ，

∴S△O′EF=18，

∵S△O′EF=O′E2，

∴O′E=6，

在RT△O′EG中，EG===3，

∴CE=CG+EG=3+3．

根据对称性可知，当∠M′ON′旋转到如图所示位置时，

CE′=E′G﹣CG=3﹣3．

综上可得，线段CE的长为3+3或3﹣3．