
【题目】综合题。
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.

(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)

(3)若AB=10,CD=3,求△ABD的面积.
【答案】(1)证明见解析;(2)如图所示见解析;(3)△ABD的面积为15.
【解析】
(1)只要证明△ACD≌△CBE即可解决问题;
(2)利用尺规作△ABC的角平分线即可;
(3)过点D作DE⊥AB于E.由DC⊥AC,DE⊥AB推出DE=DC=3,根据S△ABD=![]() ABDE计算即可;
ABDE计算即可;
(1)证明:∵∠ACB=90
∴∠ACD+∠BCE=90
∵ AD⊥l ∴∠ACD+∠CAD=90
∴∠CAD=∠BCE
∵BE⊥l,AD⊥l ∴∠ADC=∠BEC=90
∵AC=BC ∴△ACD≌△CBE
∴AD=CE,CD=BE
∵DE= CD+ CE,∴DE=AD+BE.
(2)如图所示,
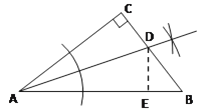
(3)解:过点D作DE⊥AB于E
∵DC⊥AC,DE⊥AB
∴DE=DC=3
∴S△ABD=![]() ABDE=
ABDE=![]() ×10×3=15.
×10×3=15.


科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对函数y=x+ ![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | m | ﹣2 | ﹣ | ﹣ |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 , m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现: ①方程x+ ![]() =3有个实数根;
=3有个实数根;
②若关于x的方程x+ ![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 . 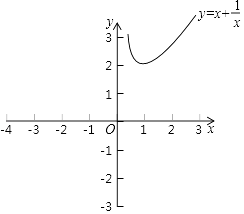
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
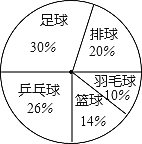
①最喜欢足球的人数最多,达到了15人;
②最喜欢羽毛球的人数最少,只有5人;
③最喜欢排球的人数比最喜欢乒乓球的人数少3人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多6人。
其中正确的结论有
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表: 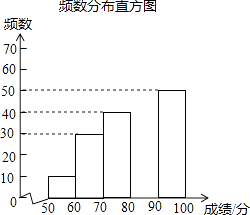
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= , n=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架长2.5m的梯子斜靠在竖直的墙上,这时梯足到墙的底端距离为0.7m,若梯子顶端下滑0.4m,则梯足将向外移
A、0.6mB、0.7m C、0.8mD、0.9m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com