
分析 由恰好使得一次函数y=(a+1)x的图象经过一、三象限的有0,1,2;使得关于x的方程x2+2x+a=0有实数解的有-2,-1,0,1,可得恰好使得一次函数y=(a+1)x的图象经过一、三象限,且使得关于x的方程x2+2x+a=0有实数解的有0,1,然后直接利用概率公式求解即可求得答案.
解答 解:∵在一个口袋中装有五个分别标有数字-2,-1,0,1,2 的小球,它们除数字不同外,其余完全相同,
∴共有5种等可能的结果,
∵恰好使得一次函数y=(a+1)x的图象经过一、三象限的有0,1,2;使得关于x的方程x2+2x+a=0有实数解的有-2,-1,0,1,
∴恰好使得一次函数y=(a+1)x的图象经过一、三象限,且使得关于x的方程x2+2x+a=0有实数解的有0,1,
∴恰好使得一次函数y=(a+1)x的图象经过一、三象限,且使得关于x的方程x2+2x+a=0有实数解的概率为:$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 此题考查了概率公式的应用以及一次函数的性质、一元二次方程根的情况.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
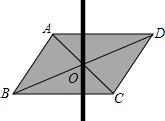 如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.
如图,用硬纸板剪一个平行四边形,作出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,使它随意停留在任意位置,观察几次拨动的结果,你发现了什么?证明你的发现.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,管中放置着三根同样的绳子AA1、BB1、CC1.
如图,管中放置着三根同样的绳子AA1、BB1、CC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com