
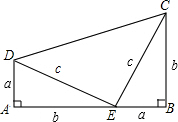
 如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性.
如图,这是美国第20届总统加菲尔德的构图,其中Rt△ADE和Rt△BEC是完全相同的,请你试用此图形验证勾股定理的正确性. 分析 此梯形的面积有三部分组成,利用梯形的面积等于三个直角三角形的面积之和列出方程并整理.
解答 证明:因为${S}_{梯形ABCD}=\frac{1}{2}•AB•(AD+BC)=\frac{1}{2}(a+b)(a+b)=\frac{1}{2}{a}^{2}+ab+\frac{1}{2}{b}^{2}$,
又因为${S}_{梯形ABCD}={S}_{△ADE}+{S}_{△DEC}+{S}_{△BEC}=\frac{1}{2}•AD•AE+\frac{1}{2}•DE•CE+\frac{1}{2}•BE•BC=\frac{1}{2}ab+\frac{1}{2}{c}^{2}+\frac{1}{2}ab=ab+\frac{1}{2}{c}^{2}$,所以$\frac{1}{2}{a}^{2}+ab+\frac{1}{2}{b}^{2}=ab+\frac{1}{2}{c}^{2}$,
得c2=a2+b2.
点评 此题考查勾股定理的证明,此类证明要转化成同一个东西的两种表示方法,从而转化成方程达到证明的结果.


科目:初中数学 来源: 题型:解答题
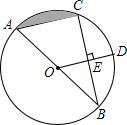 如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求:
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=2$\sqrt{3}$,DE=1,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
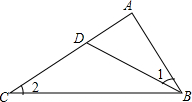 如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )
如图,下列条件:①∠1=∠2;②∠ADB=∠ABC;③AB2=AD•AC;④$\frac{AD}{AB}=\frac{BD}{BC}$,能使△ABD∽△ACB的条件的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
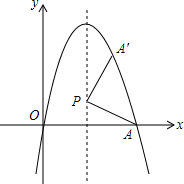 如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.
如图,经过原点的抛物线y=-x2+6x与x轴的另一个交点为A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com