
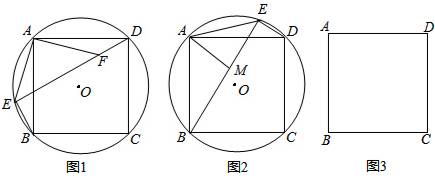
分析 (1)中易证AD=AB,EB=DF,所以只需证明∠ADF=∠ABE,利用同弧所对的圆周角相等不难得出,从而证明全等;
(2)中易证△AEF是等腰直角三角形,所以AF=AE,因为AM⊥BE,所以FM=ME=AM,EF=2AM,EF=BE-BF=BE-DE,得出结论;
(3)由PD=2可得:点P在以点D为圆心,1为半径的圆上;由∠BPD=90°可得:点P在以BD为直径的圆上.显然,点P是这两个圆的交点,由于两圆有两个交点,接下来需对两个位置分别进行讨论.然后,添加适当的辅助线,借助(2)中结论,即可解决问题.
解答 (1)证明:在正方形ABCD中,AB=AD,
∠ABE与∠ADE都对应弧AE,
∴∠ABE=∠ADE,
在△ADF和△ABE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADE}\\{BE=DF}\end{array}\right.$,
∴△ADF≌△ABE(SAS);
(2)证明:在BE上取点F,使BF=DE,连接AF,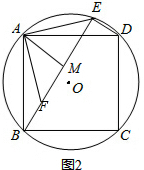
由(1)△ADE≌△ABF,
∴BF=DE,AE=AF,∠DAE=∠BAF,
在正方形ABCD中,∠BAD=90°,
∴∠BAF+∠DAF=90°,
∴∠DAE+∠DAF=90°,
∴∠EAF=90°,
∴△EAF是等腰直角三角形三角形,
∵AM⊥BE,
∴FM=ME=AM,
∴EF=2AM,
∵EF=BE-BF=BE-DE,
∴BE-DE=2AM;
(3)解:点A到BP的距离是$\sqrt{3}-\frac{1}{2}$或$\sqrt{3}+\frac{1}{2}$,
理由如下:
∵PD=2,
∴点P在以点D为圆心,2为半径的圆上,
∵∠BPD=90°,
∴点P在以BD为直径的圆上,
∴点P是这两圆的交点,
①当点P在如图3①所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,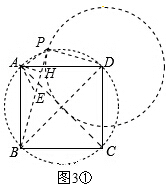
过点A作AE⊥AP,交BP于点E,如图3①,
∵四边形ABCD是正方形,
∴∠ADB=45°.AB=AD=DC=BC=2$\sqrt{2}$,∠BAD=90°,
∴BD=4.
∵DP=2,
∴BP=2$\sqrt{3}$,
∵∠BPD=∠BAD=90°,
∴A、P、D、B在以BD为直径的圆上,
∴∠APB=∠ADB=45°,
∴△PAE是等腰直角三角形,
又∵△BAD是等腰直角三角形,点B、E、P共线,AH⊥BP,
∴由(2)中的结论可得:BP=2AH+PD,
2$\sqrt{3}$=2AH+1,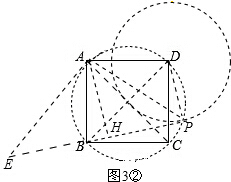
∴AH=$\sqrt{3}-\frac{1}{2}$;
②当点P在如图3②所示位置时,
连接PD、PB、PA,作AH⊥BP,垂足为H,
过点A作AE⊥AP,交PB的延长线于点E,如图3②,
同理可得:BP=2AH-PD,
2$\sqrt{3}$=2AH-2,
∴AH=$\sqrt{3}$+1,
综上所述:点A到BP的距离为$\sqrt{3}$-1或$\sqrt{3}$+1.
点评 本题考查了正方形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、圆周角定理、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力,而通过添加适当的辅助线从而能用(2)中的结论解决问题是解决第(3)的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$×$\sqrt{2}$=4 | B. | 2a3•a4=2a12 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
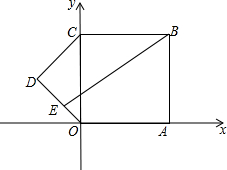 如图,平面直角坐标系中,点O为原点,点A,C分别在坐标轴上.正方形OABC边长为4,△CDO是以CO为斜边的等腰直角三角形,点E在DO上,且线段BE平分五边形OABCD的面积,则点E的坐标为(-$\frac{1}{2}$,$\frac{1}{2}$).
如图,平面直角坐标系中,点O为原点,点A,C分别在坐标轴上.正方形OABC边长为4,△CDO是以CO为斜边的等腰直角三角形,点E在DO上,且线段BE平分五边形OABCD的面积,则点E的坐标为(-$\frac{1}{2}$,$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
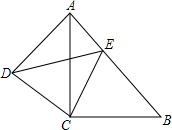 如图,在四边形ABCD中,连接AC,AC=BC,E是AB上一点,且有CE=CD,AD=BE.
如图,在四边形ABCD中,连接AC,AC=BC,E是AB上一点,且有CE=CD,AD=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两城市之间有一条国道,国道的宽为a,现要在国道上修建一座垂直于国道的立交桥,使通过A、B两城市路程最近,请你设计建桥的位置,并说明理论依据.
如图,A、B两城市之间有一条国道,国道的宽为a,现要在国道上修建一座垂直于国道的立交桥,使通过A、B两城市路程最近,请你设计建桥的位置,并说明理论依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com