
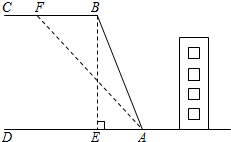
 如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:$\frac{5}{12}$,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.
如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:$\frac{5}{12}$,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.分析 (1)根据坡度的概念得到BE:EA=12:5,根据勾股定理计算列式即可;
(2)作FH⊥AD于H,根据正切的概念求出AH,结合图形计算即可.
解答 解:(1)∵斜坡AB的坡比为i=1:$\frac{5}{12}$,
∴BE:EA=12:5,
设BE=12x,则EA=5x,
由勾股定理得,BE2+EA2=AB2,即(12x)2+(5x)2=262,
解得,x=2,
则BE=12x=24,AE=5x=10,
答:改造前坡顶与地面的距离BE的长为24米;
(2)作FH⊥AD于H,
则tan∠FAH=$\frac{FH}{AH}$,
∴AH=$\frac{24}{1.33}$≈18,
∴BF=18-10=8,
答:BF至少是8米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.


科目:初中数学 来源: 题型:选择题

| A. | 边DE | B. | 边EF | C. | 边FA | D. | 边AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
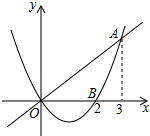 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com