
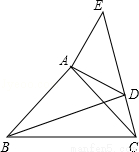
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
(1)证明见解析;(2)垂直,证明见解析.
【解析】
试题分析:要证(1)△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.
(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.
试题解析:(1)证明:∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+CAD
即∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS).
(2)BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.
∵∠DAE=90°,
∴∠E+∠ADE=90°.
∴∠ADB+∠ADE=90°.
即∠BDE=90°.
∴BD、CE特殊位置关系为BD⊥CE.
考点:全等三角形的判定与性质.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源:2015届广东省中山市八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,一次函数 的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点C的坐标;
(2)在x轴上求一点P,使它到B、C两点的距离之和最小.

查看答案和解析>>
科目:初中数学 来源:2015届广东揭阳揭西县八年级上学期期末质量检测数学试卷(解析版) 题型:选择题
下列句子中是命题的是( )
A.宽阔的大海 B.美丽的天空
C.负数都小于零 D.你的作业做完了吗?
查看答案和解析>>
科目:初中数学 来源:2015届山东省泰安市泰山区八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,将矩形纸片ABCD折叠,使边AB、CD均落在对角线BD上,得折痕BE、BF,则∠EBF= __ °.

查看答案和解析>>
科目:初中数学 来源:2015届山东省泰安市泰山区八年级下学期期末考试数学试卷(解析版) 题型:选择题
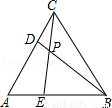
如图,在等边△ABC中,D,E分别AC,AB是上的点,且AD=BE,CE与BD交于点P,则∠BPE的度数为( )
A.75° B.60° C.55° D.45°
查看答案和解析>>
科目:初中数学 来源:2015届山东新泰龙廷镇中心学校八年级下第一次月考数学试卷(解析版) 题型:解答题
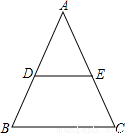
如图,在△ABC中,D是边AB的中点,DE∥BC交AC于点E.求证:AE=EC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com