
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点(0<AD<![]() AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
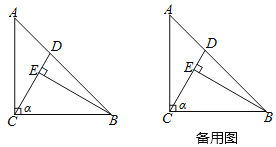
(1)①依题意补全图形.
②若α=60°,则∠CAF=_____°;![]() =_____;
=_____;
(2)用含α的式子表示EF与AB之间的数量关系,并证明.
【答案】(1)①补图见解析;②30,![]() ;(2)EF=ABcosα;证明见解析.
;(2)EF=ABcosα;证明见解析.
【解析】
(1)①利用旋转直接画出图形,
②先求出∠CBE=30°,再判断出△ACF≌△BCE,得出∠CAF=30°,再利用等腰直角三角形的性质计算即可得出结论;
(2)先判断出△ACF≌△BCE,得出∠CAF=α,再同(1)②的方法即可得出结论.
(1)①将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF,如图1;
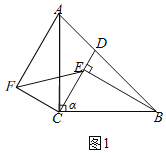
②∵BE⊥CD,∠CEB=90°,
∵α=60°,
∴∠CBE=30°,
在Rt△ABC中,AC=BC,
∴AC=![]() AB,
AB,
∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
在△ACF和△BCE中,
AC=BC,∠FCA=∠ECB,FC=EC,
∴△ACF≌△BCE(SAS),
∴∠AFC=∠BEC=90°,∠CAF=∠CBE=30°,
∴CF=![]() AC,
AC,
由旋转知,CF=CE,∠ECF=90°,
∴EF=![]() CF=
CF=![]() AC=
AC=![]() ×
×![]() AB=
AB=![]() AB,
AB,
∴![]() =
=![]() ,
,
故答案为30,![]() ;
;
(2)EF=ABcosα.
证明:∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
同(1)②的方法知,△ACF≌△BCE,
∴∠AFC=∠BEC=90°,
∴在Rt△AFC中,cos∠FCA=![]() .
.
∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°.
∵∠ECF=90°,CE=CF,
∴∠CFE=∠CEF=45°.
在△FCE和△ACB中,
∠FCE=∠ACB=90°,
∠CFE=∠CAB=45°,
∴△FCE∽△ACB,
∴![]() =cos∠FCA=cosα,
=cos∠FCA=cosα,
即EF=ABcosα.


科目:初中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 、
、![]() ,将
,将![]() 经过旋转、平移变化后得到如图1所示的
经过旋转、平移变化后得到如图1所示的![]() .
.
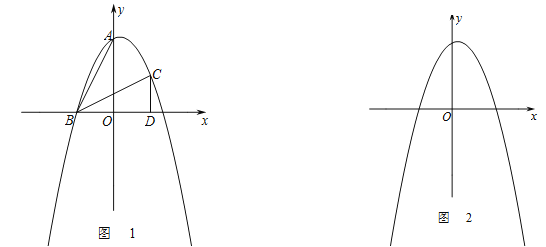
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)连结![]() ,点
,点![]() 是位于线段
是位于线段![]() 上方的抛物线上一动点,若直线
上方的抛物线上一动点,若直线![]() 将
将![]() 的面积分成
的面积分成![]() 两部分,求此时点
两部分,求此时点![]() 的坐标;
的坐标;
(3)现将![]() 、
、![]() 分别向下、向左以
分别向下、向左以![]() 的速度同时平移,求出在此运动过程中
的速度同时平移,求出在此运动过程中![]() 与
与![]() 重叠部分面积的最大值.
重叠部分面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
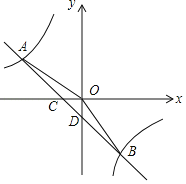
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
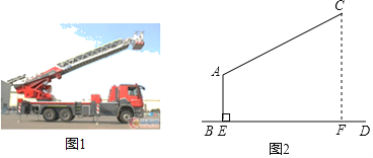
【题目】图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC是可伸缩的,其转动点A距离地面BD的高度AE为3.5m.当AC长度为9m,张角∠CAE为112°时,求云梯消防车最高点C距离地面的高度CF.(结果精确到0.1m,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40.)
查看答案和解析>>
科目:初中数学 来源: 题型:
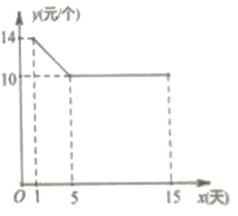
【题目】每年九月开学前后是文具盒的销售旺季,商场专门设置了文具盒专柜李经理记录了![]() 天的销售数量和销售单价,其中销售单价
天的销售数量和销售单价,其中销售单价![]() (元/个)与时间第
(元/个)与时间第![]() 天(
天(![]() 为整数)的数量关系如图所示,日销量
为整数)的数量关系如图所示,日销量![]() (个)与时间第
(个)与时间第![]() 天(
天(![]() 为整数)的函数关系式为:
为整数)的函数关系式为: 
![]() 直接写出
直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
![]() 设日销售额为
设日销售额为![]() (元) ,求
(元) ,求![]() (元)关于
(元)关于![]() (天)的函数解析式;在这
(天)的函数解析式;在这![]() 天中,哪一天销售额
天中,哪一天销售额![]() (元)达到最大,最大销售额是多少元;
(元)达到最大,最大销售额是多少元;
![]() 由于需要进货成本和人员工资等各种开支,如果每天的营业额低于
由于需要进货成本和人员工资等各种开支,如果每天的营业额低于![]() 元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com