
【题目】如图,将等腰△ABC沿DE折叠,使顶角顶点A落在其底角平分线的交点F处,若BF=DF,则∠C的度数为( )
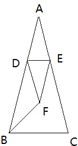
A. 60°B. 72°C. 75°D. 80°
【答案】B
【解析】
试题根据点F是底角平分线的交点,可得点F是三角形ABC角平分线的交点,连接AF,则AF平分∠BAC,设∠C=x,利用等腰三角形的性质分别得出∠BAF、∠ABF、∠AFB,然后利用三角形的内角和定理可得出答案.
如图,连接AF,
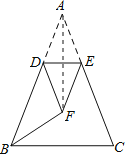
∵点F是底角平分线的交点,
∴点F是三角形ABC角平分线的交点(三角形的额角平分线交于一点),
∴AF平分∠BAC,
设∠C=x,则∠ABF=![]() x,∠BAF=
x,∠BAF=![]() ∠BAC=
∠BAC=![]() (180°-2x)=90°-x,
(180°-2x)=90°-x,
又∵BF=DF,AD=DF(折叠的性质),
∴∠FDB=∠FBD,∠DAF=∠DFA,
∴∠DFB=180°-2∠ABF=180°-x,
∴∠AFB=∠DFB+∠AFD=∠DFB+∠DAF=180°-x+(90°-x)=270°-2x,
在三角形ABF中,∠BAF+∠ABF+∠AFB=180°,即(90°-x)+(![]() x)+(270°-2x)=180°,
x)+(270°-2x)=180°,
解得:x=72°,即∠C=72°.
故选B.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+![]() .其中正确结论的序号是________________
.其中正确结论的序号是________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x轴交于点A,与y轴交于点B.动点P、Q分别从O、B同时出发,其中点P以每秒4个单位的速度沿OB向终点B运动,点Q以每秒5个单位的速度沿BA向终点A运动.设运动时间为t秒.
与x轴交于点A,与y轴交于点B.动点P、Q分别从O、B同时出发,其中点P以每秒4个单位的速度沿OB向终点B运动,点Q以每秒5个单位的速度沿BA向终点A运动.设运动时间为t秒.
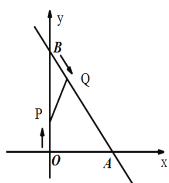
(1)连结PQ,若△AOB和以B、P、Q为顶点的三角形相似,求t的值;
(2)连结AP、OQ,若AP⊥OQ,求t的值;
(3)试证明:PQ的中点在△AOB的一条中位线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出将△ABC向下平移5个单位后得到的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整休,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0,![]() )为圆心,以
)为圆心,以![]() 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
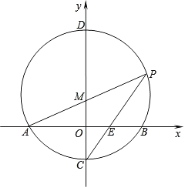
(1)求点C.P的坐标;
(2)求证:BE=2OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
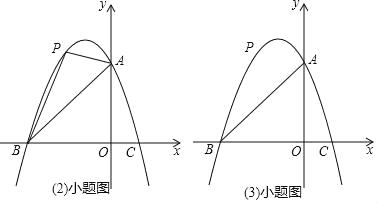
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com