【题目】如图，等边三角形△ABC的边长为4，过点C的直线
⊥AC，且△ABC与△A′B′C关于直线对称，D为线段BC′上一动点，则AD+BD的最小值是______；
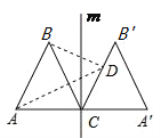
【答案】8
【解析】连接BB/，根据△ABC、△A/CB/均为正三角形即可得出A/CBB/为菱形，进而得出点B关于CB/对称的点A/，以此确定点D与点C重合时，AD+BD的最小，代入数据即可得出结论.
解：连接BB/，如图所示.
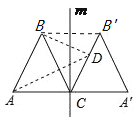
∵△ABC、△A/CB/ /均为正三角形，
∴∠ACB=∠A/=60°，A/C=BC=A/B/，
∴A/B/∥BC，
∴四边形A/CBB/ /为菱形，
∴点B关于CB/对称的点A/，
∴当点D与点C重合时，AD+BD取最小值，
此时AD+BD=4+4=8.
故答案为：8.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质，找出点B关于CB/对称的点A/是解题的关键.
全能测控期末小状元系列答案科目：初中数学 来源： 题型：
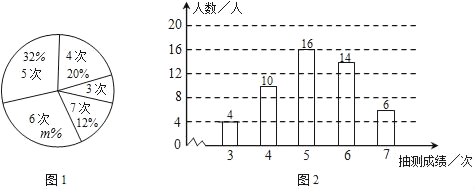
【题目】为了解某校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制出如下的统计图①和图②，请跟进相关信息，解答下列问题：
（Ⅰ）本次抽测的男生人数为 ，图①中m的值为 ；
（Ⅱ）求本次抽测的这组数据的平均数、众数和中位数；
（Ⅲ）若规定引体向上5次以上（含5次）为体能达标，根据样本数据，估计该校350名九年级男生中有多少人体能达标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用无刻度的直尺按要求作图，请保留画图痕迹，不需要写作法．
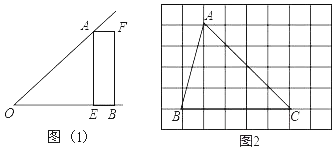
（1）如图1，已知∠AOB，OA＝OB，点E在OB边上，四边形AEBF是矩形．请你只用无刻度的直尺在图中画出∠AOB的平分线．
（2）如图2，在8×6的正方形网格中，请用无刻度直尺画一个与△ABC面积相等，且以BC为边的平行四边形，顶点在格点上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△AEC和△DFB中，∠E＝∠F，点A，B，C，D在同一直线上，有如下三个关系式：①AE∥DF，②AB＝CD，③CE＝BF.
(1)请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题(用序号写出命题书写形式：“如果，，那么”)；
(2)选择(1)中你写出的一个命题，说明它正确的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司仓库本周内货物进出的吨数记录如下
“
”表示进库，“
”表示出库
；
日期 | 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
吨数 |
|
|
|
|
|
|
|
这一周，仓库内货物的总吨数是______了填“增多”或“减少”；
若周六结束时仓库内还有货物360吨，则周日开始时仓库内有货物多少吨？
如果该仓库货物进出的装卸费都是每吨5元，那么这一周内共需付多少元的装卸费？
查看答案和解析>>
科目：初中数学 来源： 题型：
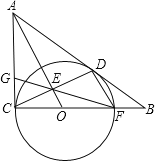
【题目】如图，⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D，与边BC相交于点F，OA与CD相交于点E，连接FE并延长交AC边于点G．
（1）求证：DF∥AO；
（2）若AC=6，AB=10，求CG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，甲、乙两个容器内都装了一定数量的水，现将甲容器中的水匀速注入乙容器中．图2中的线段AB，CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象．下列结论错误的是( )
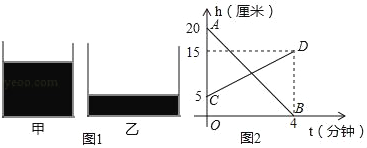
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时，甲、乙两个容器中的水的深度相等
D. 注水1分钟时，甲容器的水比乙容器的水深5厘米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】指出下列近似数精确到哪个数位：
（1）π≈3.14 精确到______． （2）
精确到____；
（3）21.80≈______（精确到个位）；（4）579700 精确到千位是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
