练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，对角线AC与BD相交于点O，P为AD上的动点，过点P作PM⊥AC，PN⊥BD，垂足分别为M、N，若AB=m，BC=n，则PM+PN=（　　）

    A.B.C.D.

    【答案】C

    【解析】

    连接OP，由矩形的性质得出OA=OD，∠ABC=90°，由勾股定理求出AC，得出OA，由△OAP的面积+△ODP的面积=矩形ABCD的面积，即可得出结果．

    连接OP，如图所示：

    ∵四边形ABCD是矩形，

    ∴∠ABC=90°，OA=AC，OD=BD，AC=BD，

    ∴OA=OD，AC=，

    ∴OA=OD=，

    ∵△OAP的面积+△ODP的面积=△AOD的面积=矩形ABCD的面积，

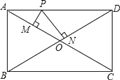
    即OAPM+ODPN=OA（PM+PN）=ABBC=mn，

    ∴PM+PN=，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与CD相交于点O，OE平分∠AOD，OF平分∠BOD.

    (1)若∠AOC＝70°，求∠DOE和∠EOF的度数；

    (2)请写出图中∠AOD的补角和∠AOE的余角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．

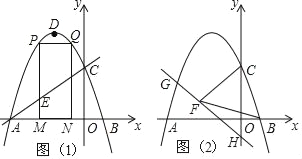
    （1）求抛物线的解析式；

    （2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；

    （3）已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图的2016年6月份的日历表中，任意框出表中竖列上三个相邻的数，这三个数的和不可能是(　 　)

    A. 27 B. 51 C. 69 D. 72

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明在大楼45米高（即PH=45米，且PH⊥HC）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的

    坡度i（即tan∠ABC）为1： .（点P、H、B、C、A在同一个平面上

    点H、B、C在同一条直线上）

    （1）∠PBA的度数等于________度；

    （2）求A、B两点间的距离（结果精确到0.1米，参考数据： ≈1.414， ≈1.732）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正比例函数y=kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3．

    （1）求正比例函数的解析式；

    （2）在x轴上能否找到一点P，使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有若干根长度相同的火柴棒，用a根火柴棒，按如图①摆放时可摆成m个正方形，用b根火柴棒，按如图②摆放时可摆成2n个正方形．(m、n是正整数)

    （1）如图①，当m=4时，a=______；如图②，当b=52时，n=______；

    （2）当若干根长度相同的火柴棒，既可以摆成图①的形状，也可以摆成图②的形状时，m与n之间有何数量关系，请你写出来并说明理由；

    （3）现有61根火柴棒，用若干根火柴棒摆成图①的形状后，剩下的火柴棒刚好可以摆成图②的形状．请你直接写出一种摆放方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在6×6的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，作△ABC的外接圆⊙O，则弧AC的长等于（　　）

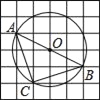
    A. π B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD与正方形BFGE中，点E在边AB上，若AE=a，BE=b，（其中a＞2b）．

    （1）请用含有a，b的代数式表示图中阴影部分的面积；

    （2）当a=5cm，b=3cm时，求阴影部分的面积．

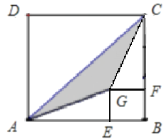
    查看答案和解析>>

    同步练习册答案