
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A'B'C是由△ABC绕点C顺时针旋转所得,连接AB',且点A,B',A'在同一条直线上,则AA'的长为__.

【答案】3
【解析】
根据直角三角形的性质,可得AB的长,根据旋转的性质,可得A′B′的长,B′C的长,∠A′、∠A′B′C′,根据邻补角的定义,可得∠AB′C的度数,根据等腰三角形的判定,可得AB′,根据线段的和差,可得答案.
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴AB=2BC=2×1=2,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=2,B′C=BC=1,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=1,
∴AA′=AB′+A′B′=2+1=3.


科目:初中数学 来源: 题型:
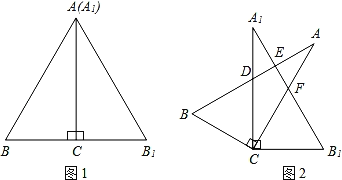
【题目】将两块全等的含30°角的直角三角扳按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转(如图2所示),AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.给出下列结论:
①当旋转角等于20°时,∠BCB1=l60°;
②当旋转角等于30°时,AB与A1B1垂直;
③当旋转角等于45°时,AB∥CB1;
④当AB∥CB1时,点D为A1C的中点.
其中正确的是_____(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
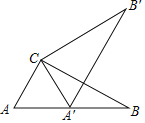
A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
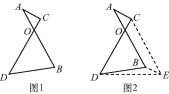
【题目】王老师在黑板上写了一道题:如图1,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,试比较AC+BD与AB的大小.小聪思考片刻就想出来了,他说将AB平移到CE位置,如图2,连接BE,DE,就可以比较AC+BD与AB的大小了,你知道他是怎样比较的吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
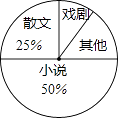
(1)计算m=;
(2)在扇形统计图中,“其他”类所占的百分比为;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD, ![]() ,
,![]() .求
.求![]() 度数.
度数.
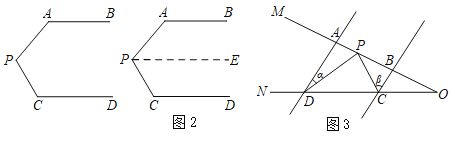
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得![]() _______.
_______.
问题迁移:如图3,AD∥BC,点P在射线OM上运动, ![]() ,
, ![]() .
.
(1)当点P在A、B两点之间运动时, ![]() 、
、![]() 、
、![]() 之间有何数量关系?请说明理由.
之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com