
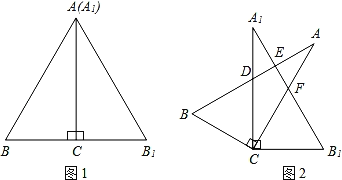
【题目】将两块全等的含30°角的直角三角扳按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转(如图2所示),AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.给出下列结论:
①当旋转角等于20°时,∠BCB1=l60°;
②当旋转角等于30°时,AB与A1B1垂直;
③当旋转角等于45°时,AB∥CB1;
④当AB∥CB1时,点D为A1C的中点.
其中正确的是_____(写出所有正确结论的序号).
【答案】①②④
【解析】
求出∠BCB1+A1CA=180°,求出∠A1CA和∠BCB1,再判断①②③即可;根据两直线平行,同旁内角互补求出∠ADC=90°,再根据直角三角形30°角所对的直角边等于斜边的一半可得CD=![]() AC,根据旋转的性质可得A1C=AC,然后求出解,即可判断④.
AC,根据旋转的性质可得A1C=AC,然后求出解,即可判断④.
①∵∠ACB=∠A1CB1=90°,
∴∠BCB1+A1CA=∠ACB+∠ACB1+∠A1CA=∠ACB+∠A1CB1=90°+90°=180°,
∵旋转角等于20°,
∴∠A1CB=90°﹣20°=70°,
∴∠A1CA=90°﹣70°=20°,
∴∠BCB1=180°﹣∠A1CA=160°,
∴①正确;
②∵两块全等的含30°角的直角三角扳按图I的方式放置,
∴∠B=∠B1=60°,
∵旋转角等于30°,
∴∠A1CB=90°﹣30°=60°,
∴∠A1CA=90°﹣60°=30°,
∴∠BCB1=180°﹣∠A1CA=150°,
∴∠BEB1=360°﹣60°﹣60°﹣150°=90°,
∴AB与A1B1垂直,
∴②正确;
③∵旋转角等于45°,
∴∠A1CB=90°﹣45°=45°,
∴∠A1CA=90°﹣45°=45°,
∴∠BCB1=180°﹣∠A1CA=145°,
∴∠BEB1+∠B=135°+60°=195°≠180°,
∴AB和CB1不平行,
∴③错误;
④∵AB∥CB1,
∴∠ADC=180°﹣∠A1CB1=180°﹣90°=90°,
∵∠BAC=30°,
∴CD=![]() AC,
AC,
又∵由旋转的性质得,A1C=AC,
∴A1D=CD,
∴④正确;
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )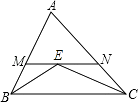
A.12
B.4
C.8
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
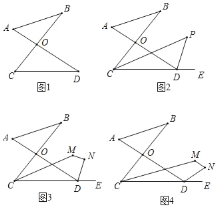
【题目】(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,DP交于点P,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,∠ADE,当∠A+∠B=80°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=![]() ∠BCD,∠NDE=
∠BCD,∠NDE=![]() ∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
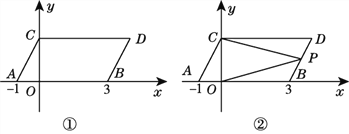
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A'B'C是由△ABC绕点C顺时针旋转所得,连接AB',且点A,B',A'在同一条直线上,则AA'的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com