
����Ŀ�����꼶һ�չ�ˡ���һ�����顱�Ļ����ί���ѧ���Ķ��鼮������������ʾ����飬�ʾ������ˡ�С˵������Ϸ�硱����ɢ�ġ�����������
�ĸ����ÿλͬѧ��ѡһ����ݵ����������˲�������Ƶ���ֲ���������ͳ��ͼ������ͼ���ṩ����Ϣ���ش��������⣺
��� | Ƶ���������� | Ƶ�� |
С˵ | 0.5 | |
Ϸ�� | 4 | |
ɢ�� | 10 | 0.25 |
���� | 6 | |
�ϼ� | m | 1 |
��1������m=��
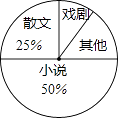
��2��������ͳ��ͼ�У�������������ռ�İٷֱ�Ϊ��
��3���ڵ����ʾ��У��ס��ҡ���������λͬѧѡ���ˡ�Ϸ�硱�࣬�ִ�������ѡ��2��ͬѧ�μ�ѧУ��Ϸ�����ţ����û���״ͼ���б��ķ�������ѡȡ��2��ǡ�����Һͱ��ĸ��ʣ�
���𰸡�
��1��40
��2��15%
��3���⣺����״ͼ����ͼ��ʾ��
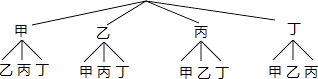
���еȿ��ܵ������12�֣�����ǡ���DZ����ҵ������2�֣�
��P�������ң�= ![]() =
= ![]()
���������⣺��1����ϲ��ɢ�ĵ���10�ˣ�Ƶ��Ϊ0.25��
��m=10��0.25=40��2��������ͳ��ͼ�У�������������ռ�İٷֱ�Ϊ ![]() ��100%=15%��
��100%=15%��
�ʴ�Ϊ��15%��
��1������ϲ��ɢ����������Ƶ�ʣ����ɵó�m��ֵ��
��2���á������������������40���������ռ�ٷֱȡ�
��3���������ڲ��Żأ��г���״ͼ��������еȿ�������ǡ���DZ����ҵ�����Ŀ����������ݸ��ʹ�ʽ������⡣



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���½���һ����ҵ��ÿ�½�����1960����ˮ��Ϊ��������������ҵ�ƻ�������ˮ���������������������ͺ���ѡ��
��ˮ�������ͺ� | A�� | B�� |
������ˮ��������/�£� | 240 | 180 |
��֪�̼��۳���2̨A�͡�3̨B����ˮ���������ܼ�Ϊ44��Ԫ���۳���1̨A�͡�4̨B����ˮ���������ܼ�Ϊ42��Ԫ��
��1����ÿ̨A�͡�B����ˮ�������ļ۸�
��2��Ϊȷ����ÿ�²�������ˮȫ�������꣬����ҵ����������������ˮ����������ô��������Ҫ֧������Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
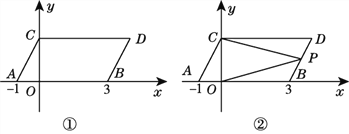
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ(��1��0)��(3��0)����ͬʱ����A��B�ֱ�����ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD.
(1)���C��D�����꼰S�ı���ABDC.
(2)��y�����Ƿ����һ��Q������QA��QB��ʹS��QAB��S�ı���ABDC������������һ�㣬�����Q�����ꣻ�������ڣ���˵�����ɣ�
(3)��ͼ�ڣ���P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ(����B��D�غ�)���������н��ۣ���![]() ��ֵ���䣬��
��ֵ���䣬��![]() ��ֵ���䣬��������ֻ��һ������ȷ�ģ������ҳ�������۲�����ֵ��
��ֵ���䣬��������ֻ��һ������ȷ�ģ������ҳ�������۲�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��Rt��ABC��,��ACB=90��,��B=60��,BC=1,��A'B'C���ɡ�ABC�Ƶ�C˳ʱ����ת����,����AB',�ҵ�A,B',A'��ͬһ��ֱ����,��AA'�ij�Ϊ__.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬ADƽ�֡�CAB����CB�ڵ�D������D��DE��AB�ڵ�E��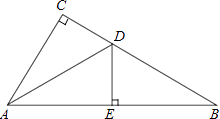
��1����֤����ACD�ա�AED��
��2������B=30�㣬CD=1����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA=3��OC=2��F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y=kx��1��k��0����ͼ����BC�߽��ڵ�E����FΪAB���е�ʱ����ú����Ľ���ʽ��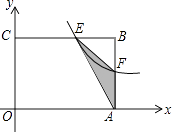
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y=-2x+4�����н��۴������(����)
A. ������ͼ����x��Ľ���������![]()
B. ����ֵ���Ա������������С
C. ������ͼ������������
D. ������ͼ������ƽ��4����λ���ȵ�![]() ��ͼ��
��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�BC=a��AC=b��AB=c������C=90�㣬��ͼ��1�������ݹ��ɶ�������a2+b2=c2������ABC����ֱ�������Σ���ͼ��2����ͼ��3����������ȹ��ɶ������Բ���a2+b2��c2�Ĺ�ϵ����֤����Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1+��2��180�㣬��3����B����˵��DE��BC�������Dz����Ƶ����̣������������������Ƶ����ݻ����ݣ�
֤�����ߡ�1+��2��180�㣨��֪��
��1����4 ���� ����
���2+��4��180�㣨����������
��EH��AB���� ����
���B���� ������ ����
�ߡ�3����B����֪��
���3����EHC������������
��DE��BC ���� ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com