
【题目】如图:在△ABC中,CD是AB边上的高,AC=20,BC=15,DB=9. 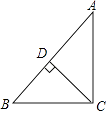
(1)求CD的长;
(2)△ABC是直角三角形吗?为什么?
【答案】
(1)解:∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,BC=15,DB=9,
根据勾股定理得:CD= ![]()
(2)解:△ABC为直角三角形,理由为:
在Rt△ACD中,AC=20,CD=12,
根据勾股定理得:AD= ![]() ;
;
∵AB=BD+AD=9+16=25,
∴AC2+BC2=AB2,
∴△ABC为直角三角形
【解析】(1)由CD垂直于AB,得到三角形BCD与三角形ACD都为直角三角形,由BC与DB,利用勾股定理求出CD的长;(2)三角形ABC为直角三角形,理由为:由BD+AD求出AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形.
【考点精析】认真审题,首先需要了解勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形).


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图:
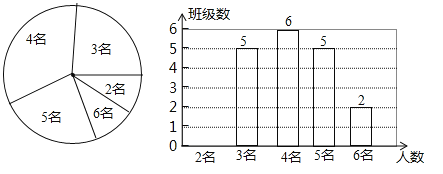
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=﹣x+b的图象与x轴、y轴的交点分别为A、B与反比例函数![]() 的图象交于点C、D,且
的图象交于点C、D,且![]() .
.
(1)求∠BAO的度数;
(2)求O到DC的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= 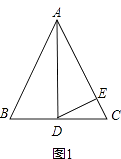
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= 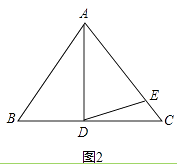
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由. 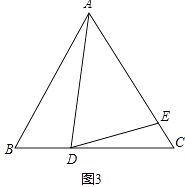
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.邻边之比相等的两个平行四边形一定相似B.邻边之比相等的两个矩形一定相似
C.对角线之比相等的两个平行四边形一定相似D.对角线之比相等的两个矩形一定相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的三边是三个连续的奇数,最长边是2k+5(k为大于1的整数),则其它两边分别分别是 和 ,猜想:这个三角形的最长边与最短边之和与第三边有何关系,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数是a,在它的左边加上一个数字b变成一个三位数,则这个三位数用代数式表示为( )
A. 10a+100b B. ba C. 100ba D. 100b+a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com