��ת��ļ���������ȫ�����ص��п��Ծ��г��ֵ�Ƶ�ʺܴ����С��ͬѧ���ij����ѧ�п����ĵ����ڶ�����������������ר�ŵ��о������ܺ�С��һ�������и������𣿣����¸���ֻҪ��д����Ҫ�ļ�����̺ͼ�������˵�����ɣ���
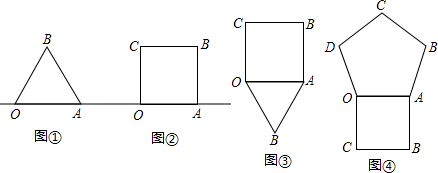
��1����ͼ�٣�С��ͬѧ��һ���߳�Ϊ1����������ֽƬ������OAB������ֱ��l
1�ϣ�OA����ֱ��l
1�غϣ�Ȼ��������ֽƬ���ҷ�תһ�ܻص���ʼλ�ã���O��������·�̣�
��2��С�ƽ�������о�����ͼ�ڣ����ѱ߳�Ϊ1��������ֽƬOABC����ֱ��l
2�ϣ�OA����ֱ��l
2�غϣ�Ȼ��������ֽƬ���ҷ�ת���ɴΣ���������������⣺
����٣���������ֽƬOABC������������תһ�ܻص���ʼλ�ã���O������·�̣�
����ڣ�������ֽƬOABC��������������
����ת������O������·����
�У�
��3����С���ֽ����˽�һ������չ�о�����������������ε�һ��OA����������ε�һ��OA�غϣ���ͼ3����Ȼ������������������������Ϸ�ת��ֱ���������ε�һ�λص���ʼλ�ã���O�㣬A�㣬B������λ�úͳ�ʼʱһ��������O����������·�̣�
�����ѱ߳�Ϊ1��������OABC���ڱ߳�Ϊ1���������OABCD�Ϸ�ת����ͼ�ܣ���ֱ�������ε�һ�λص���ʼλ�ã���O�㣬A�㣬B�㣬C������λ�úͳ�ʼʱһ��������O����������·�̣�




 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
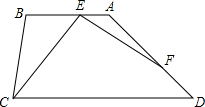 ��ͼ������ABCD��AB��CDƽ�У���BCD=2��D=2������CEF=��B��
��ͼ������ABCD��AB��CDƽ�У���BCD=2��D=2������CEF=��B��