
【题目】如图,已知A(﹣4, ![]() ),B(﹣1,2)是一次函数y=kx+b与反比例函数
),B(﹣1,2)是一次函数y=kx+b与反比例函数 ![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
【答案】
(1)解:当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(2)把A(﹣4, ![]() ),B(﹣1,2)代入y=kx+b得
),B(﹣1,2)代入y=kx+b得 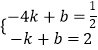 ,
,
解得 ![]() ,
,
所以一次函数解析式为y= ![]() x+
x+ ![]() ,
,
把B(﹣1,2)代入y= ![]() 得m=﹣1×2=﹣2;
得m=﹣1×2=﹣2;
(3)解:如下图所示:

设P点坐标为(t, ![]() t+
t+ ![]() ),
),
∵△PCA和△PDB面积相等,
∴ ![]()
![]() (t+4)=
(t+4)= ![]() 1(2﹣
1(2﹣ ![]() t﹣
t﹣ ![]() ),即得t=﹣
),即得t=﹣ ![]() ,
,
∴P点坐标为(﹣ ![]() ,
, ![]() ).
).
【解析】(1)观察函数图象得到当﹣4<x<﹣1时,一次函数图象都在反比例函数图象上方;(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y= ![]() 可计算出m的值;(3)设P点坐标为(t,
可计算出m的值;(3)设P点坐标为(t, ![]() t+
t+ ![]() ),利用三角形面积公式可得到
),利用三角形面积公式可得到 ![]()
![]() (t+4)=
(t+4)= ![]() 1(2﹣
1(2﹣ ![]() t﹣
t﹣ ![]() ),解方程得到t=﹣
),解方程得到t=﹣ ![]() ,从而可确定P点坐标.
,从而可确定P点坐标.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( ) 
A.80°
B.110°
C.120°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.
(1)请用列表或画树状图的方法写出所有的可能;
(2)求一次函数y=kx+b的图象经过一、二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A,B对应的数分别是x,y,且|x+100|+(y﹣200)2=0,点P为数轴上从原点出发的一个动点,速度为30单位长度/秒.
(1)求点A,B两点之间的距离;
(2)若点A向右运动,速度为10单位长度/秒,点B向左运动,速度为20单位长度/秒,点A,B和P三点同时开始运动,点P先向右运动,遇到点B后立即掉后向左运动,遇到点A再立即掉头向右运动,如此往返,当A,B两点相距30个单位长度时,点P立即停止运动,求此时点P移动的路程为多少个单位长度?
(3)若点A,B,P三个点都向右运动,点A,B的速度分别为10单位长度/秒,20单位长度/秒,点M、N分别是AP、OB的中点,设运动的时间为t(0<t<10),在运动过程中①![]() 的值不变;②
的值不变;②![]() 的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,分别在AB,BC的延长线上截取点G,H,使BG=BH,延长AC交GH于点K,且AK=KG,则∠BAC的大小等于( )
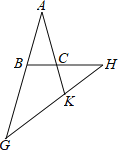
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:( ![]() ﹣1)0+2sin30°﹣(
﹣1)0+2sin30°﹣( ![]() )﹣1+|﹣2017|;
)﹣1+|﹣2017|;
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1 , 若∠A=100°,求证:A1C1∥BC. 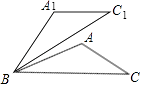
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com