
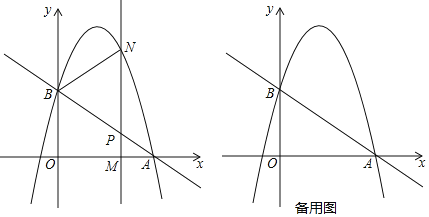
【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.
【答案】(1)![]() ,
,![]() ;(2)N(
;(2)N(![]() ,
,![]() );(3)M(
);(3)M(![]() ,0)或M(
,0)或M(![]() ,0) .
,0) .
【解析】分析: (1)利用待定系数法求直线和抛物线解析式;
(2)先表示出N(m,- ![]() m2+
m2+![]() m+2),P(m,-
m+2),P(m,-![]() m+2),则计算出NP=-
m+2),则计算出NP=-![]() m2+4m,PM=-
m2+4m,PM=-![]() m+2,则利用NP=PM得到-
m+2,则利用NP=PM得到-![]() m2+4m=-
m2+4m=-![]() m+2,然后解方程求出m即可得到N点坐标;
m+2,然后解方程求出m即可得到N点坐标;
(3)利用两点间的距离公式计算出AB=![]() ,BP=
,BP=![]() m,NP=-
m,NP=-![]() m2+4m,由于∠BPN=∠ABO,利用相似三角形的判定方法,当
m2+4m,由于∠BPN=∠ABO,利用相似三角形的判定方法,当![]() 时,△BPN∽△OBA,则△BPN∽△MPA,即
时,△BPN∽△OBA,则△BPN∽△MPA,即 ;当
;当![]() 时,△BPN∽△ABO,则△BPN∽△APM,即
时,△BPN∽△ABO,则△BPN∽△APM,即 ,然后分别解关于m的方程即可得到对应的M点的坐标.
,然后分别解关于m的方程即可得到对应的M点的坐标.
详解:
(1)解:设直线![]() 的解析式为
的解析式为![]() (
(![]() )
)
∵![]() ,
, ![]()
∴![]() 解得
解得
∴直线![]() 的解析式为
的解析式为![]()
∵抛物线![]() 经过点
经过点![]() ,
, ![]()
∴ 解得
解得
∴![]()
(2)∵![]() 轴,
轴, ![]() 设
设![]() ,
, ![]()
∴![]() ,
, ![]()
∵![]() 点是
点是![]() 的中点
的中点
∴![]()
∴![]()
解得![]() ,
, ![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
(3)∵![]() ,
, ![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵![]()
∴当![]() 与
与![]() 相似时,存在以下两种情况:
相似时,存在以下两种情况:
![]()
∴ 解得
解得![]()
∴![]()
![]()
∴ ,解得
,解得![]()
∴![]()
点睛: 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质;会利用待定系数法求函数解析式;灵活应用相似比表示线段之间的关系;理解坐标与图形的性质;会利用分类讨论的思想解决数学问题.


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与射线
与射线![]() 平行,
平行,![]() .点
.点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() 平分
平分![]() ,点
,点![]() 都在点
都在点![]() 的右侧.
的右侧.

![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 把题中条件“射线
把题中条件“射线![]() ”改为“直线
”改为“直线![]() ” ,条件点
” ,条件点![]() 都在点
都在点![]() 的右侧”改为“点
的右侧”改为“点![]() ,
,![]() ,都在点
,都在点![]() 的左侧”,请你在图2中画出
的左侧”,请你在图2中画出![]() ,并直接写出
,并直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线![]() 上有三点
上有三点![]() 、
、![]() 、
、![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度匀速运动,点
的速度匀速运动,点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上向点
上向点![]() 匀速运动,两点同时出发,当点
匀速运动,两点同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 、
、![]() 停止运动.
停止运动.


(1)若点![]() 运动速度为
运动速度为![]() ,经过多长时间
,经过多长时间![]() 、
、![]() 两点相遇?
两点相遇?
(2)当![]() 时,点
时,点![]() 运动到的位置恰好是线段
运动到的位置恰好是线段![]() 的中点,求点
的中点,求点![]() 的运动速度;
的运动速度;
(3)设运动时间为![]() ,当点
,当点![]() 运动到线段
运动到线段![]() 上时,分别取
上时,分别取![]() 和
和![]() 的中点
的中点![]() 、
、![]() ,则
,则![]() ____________
____________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
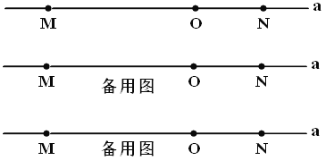
【题目】如图,直线![]() 上有
上有![]() 、
、![]() 两点,
两点,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
(1)填空:![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)若点![]() 是线段
是线段![]() 上一点,且满足
上一点,且满足![]() ,求
,求![]() 的长;
的长;
(3)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,向右运动,点
两点同时出发,向右运动,点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .设运动时间为
.设运动时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 、
、![]() 两点停止运动.
两点停止运动.
①当![]() 为何值时,
为何值时,![]() ?
?
②当点![]() 经过点
经过点![]() 时,动点
时,动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度也向右运动,当点
的速度也向右运动,当点![]() 追上点
追上点![]() 后立即返回,以
后立即返回,以![]() 的速度向点
的速度向点![]() 运动,遇到点
运动,遇到点![]() 后再立即返回,以
后再立即返回,以![]() 的速度向点
的速度向点![]() 运动,如此往返,直到点
运动,如此往返,直到点![]() 、
、![]() 停止运动时,点
停止运动时,点![]() 也停止运动.求出在此过程中点
也停止运动.求出在此过程中点![]() 运动的总路程是多少?
运动的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.
(1)当0≤x≤200,且x为整数时,y关于x的函数解析式为【1】;当200≤x≤300,且x为整数时,y关于x的函数解析式为【2】;
(2)要使游乐场一天的赢利超过1000元,试问该天至少应售出多少张门票;
(3)请思考并解释图象与y轴交点(0,﹣1000)的实际意义;
(4)根据图象,请你再提供2条信息.

查看答案和解析>>
科目:初中数学 来源: 题型:
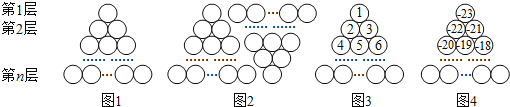
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]() ,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
,图3图4的中的圆圈共有14层.我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是__________;我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,则图4中所有圆圈中各数的绝对值之和为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com