
【题目】学了一元二次方程的根与系数的关系后,小亮兴奋地说:“若设一元二次方程的两个根为x1,x2,就能快速求出![]() +
+![]() ,x12+x22,…的值了.比如设x1,x2是方程x2+2x-3=0的两个根,则x1+x2=-2,x1x2=-3,得
,x12+x22,…的值了.比如设x1,x2是方程x2+2x-3=0的两个根,则x1+x2=-2,x1x2=-3,得![]() +
+![]() =
=![]() =
=![]() .”
.”
(1)小亮的说法对吗?简要说明理由;
(2)写一个你最喜欢的一元二次方程,并求出两根的平方和.
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象既是_________图形又是_________图形,它有_________条对称轴,且对称轴互相_________,对称中心是_________.
的图象既是_________图形又是_________图形,它有_________条对称轴,且对称轴互相_________,对称中心是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?

(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
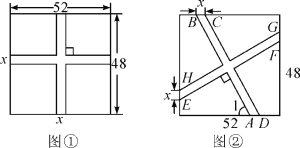
小亮设计的方案如图①所示,甬路宽度均为x m,剩余的四块绿地面积共2300 m2.
小颖设计的方案如图②所示,BC=HE=x,AB∥CD,HG∥EF,AB⊥EF,∠1=60°.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线a、b、c上,且a、b之间的距离为1,b、c之间的距离为2,则AC2=( )

A.13B.20C.25D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com