
【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?

(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
【答案】(1) (x+0.7)2+22=2.52 ,0.8,-2.2(舍去),0.8 ;(2)【问题一】不会是0.9米,理由见解析;【问题二】有可能,理由见解析.
【解析】
(1)直接把B1C、A1C、A1B1的值代入进行解答即可;
(2)把(1)中的0.4换成0.9可知原方程不成立;设梯子顶端从A处下滑x米,点B向外也移动x米代入(1)中方程,求出x的值符合题意.
(1) (x+0.7)2+22=2.52, 0.8 , -2.2(舍去), 0.8;
(2) 【问题一】不会是0.9米.若AA1=BB1=0.9,则A1C=2.4-0.9=1.5,B1C=0.7+0.9=1.6, 1.52+1.62=4.81,2.52=6.25,
∵A1C2+B1C2≠A1B12,
∴该题的答案不会是0.9米;
【问题二】
有可能.设梯子顶端从A处下滑x米,点B向外也移动x米,则有(x+0.7)2+(2.4-x)2=2.52,解得x=1.7或x=0(舍去).
∴当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.


科目:初中数学 来源: 题型:
【题目】已知:![]() ,OE平分
,OE平分![]() ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点![]() 、B、C不与点O重合
、B、C不与点O重合![]() ,连接AC交射线OE于点
,连接AC交射线OE于点![]() 设
设![]() .
.

![]() 如图1,若
如图1,若![]() ,则
,则
![]() 的度数是______;
的度数是______;
![]() 当
当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______.
______.
![]() 如图2,若
如图2,若![]() ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得![]() 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
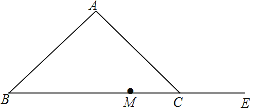
【题目】如图,在△ABC中,AB=AC.
(1)尺规作图:作∠ABC的平分线,交AC于点D(保留作图痕迹,不写作法);
(2)E是底边BC的延长线上一点,M是BE的中点,连接DE,DM,若CE=CD,求证:DM⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学了一元二次方程的根与系数的关系后,小亮兴奋地说:“若设一元二次方程的两个根为x1,x2,就能快速求出![]() +
+![]() ,x12+x22,…的值了.比如设x1,x2是方程x2+2x-3=0的两个根,则x1+x2=-2,x1x2=-3,得
,x12+x22,…的值了.比如设x1,x2是方程x2+2x-3=0的两个根,则x1+x2=-2,x1x2=-3,得![]() +
+![]() =
=![]() =
=![]() .”
.”
(1)小亮的说法对吗?简要说明理由;
(2)写一个你最喜欢的一元二次方程,并求出两根的平方和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.

(1)试说明:△ADF是直角三角形;
(2)求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为推进书香校园建设,在全校范围开展图书漂流活动,现需要购进一批甲、乙两种规格的漂流书屋放置图书.已知一个甲种规格的漂流书屋的价格比一个乙种规格的漂流书屋的价格高80元;如果购买2个甲种规格的漂流书屋和3个乙种规格的漂流书屋,一共需要花费960元.
(1)求每个甲种规格的漂流书屋和每个乙种规格的漂流书屋的价格分别是多少元?
(2)如果学校计划购进这两种规格的漂流书屋共15个,并且购买这两种规格的漂流书屋的总费用不超过3040元,那么该学校至多能购买多少个甲种规格的漂流书屋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com