Question

20．已知A（-2，2）为正比例函数y=kx上一点，试问在x轴上是否存在一点P，使A，P和坐标原点O构成等腰直角三角形？若存在，试求出P点的坐标；若不存在，试说明理由．

Answer 1

分析 过A作AN⊥y轴于N，作AM⊥x轴于M，求出四边形AMON是正方形，求出AN=ON=OM=AM=2，分为两种情况：①∠APO=90°，②∠PAO=90°，求出OP即可．

解答 解：在x轴上存在一点P，使A，P和坐标原点O构成等腰直角三角形，
把A（-2，2）代入y=kx得：k=-1，
即函数的解析式为y=-x，
过A作AN⊥y轴于N，作AM⊥x轴于M，
则∠ANO=∠NOM=∠AMO=90°，
ON=OM=2，
所以四边形AMON是正方形，
即AN=ON=OM=AM=2，
分为两种情况：①如图1，当∠APO=90°时，即P和M重合，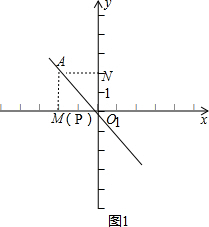
所以此时P的坐标是（-2，0）；
②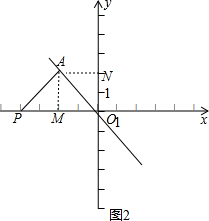
如图2，当∠PAO=90°时，
∵四边形AMON是正方形，
∴∠AOM=∠OAM=45°，
∴∠PAM=45°，
∴∠PAM=∠APM=45°，
∴PM=AM=2，
∴OP=2+2=4，
∴P的坐标是（-4，0）；
∵∠AOM=45°，P在x轴上，
∴∠AOP的度数是45°或135°，
即只有以上两种情况，
即P的坐标是（-2，0）或（-4，0）．

点评 本题考查了等腰直角三角形的性质，正方形的性质和判定，一次函数的图象上点的坐标特征的应用，能进行分类讨论是解此题的关键．